Cp and Cpk are considered short-term potential capability measures for a process. In Six Sigma, we want to describe the process quality in terms of sigma because this gives us an easy way to talk about how capable different processes are using a common mathematical framework. In other words, it allows us to compare an apple process to an orange process!
Process Capability
This is a long article, but I thought it was important to keep Cp and Cpk together. First, I’ll address Cpk, then Cp. There are also crib notes on what the equations mean in a real performance sense, what you should be able to tell about a process depending on Cp and Cpk values, and more. Please let me know in the notes below if you do not find what you are looking for.
Before We Begin!
I wrote this article to help Six Sigma Green Belt and Black Belt candidates prepare for and pass their exams.
If that’s you, leave me a comment below or contact me and let me know which organization and belt you’re studying for. This will help me make the article even better for you.
If you’re studying for something else, please leave a comment or contact me and let me know what you are studying for. Again, this will help me improve the article for you and everyone else. Thanks, Ted.
What is the Difference between Cp, Cpk and Pp, PPk?
Cp and Cpk are called Process Capability. Pp and Ppk are called Process Performance. In both cases, we want to try to verify if the process can meet Customer CTQs (requirements).
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!Cp and Cpk are used for Process Capability. Generally, you use this when a process is under statistical control. This often happens with a mature process that has been around for a while. Process capability uses the process sigma value determined from either the Moving Range, Range, or Sigma control charts.
Pp and PPk are used for Process Performance. Generally, you use this when a process is too new to determine if it is under statistical control. Ex. you are piloting a new process or testing a short pre-production run. Because there is not a lot of historical data, we take large samples from the process to account for variation. Process Performance generally uses sample sigma in its calculation.
In theory, Cpk will always be greater than or equal to Ppk. There are anomalies seen when the sample size is small, and the data represents a short amount of time where estimating using R will overstate standard deviation and make Cpk smaller than Ppk. It is not real; there can never be less variation in the long term since the long term is using all of the data, not just two pieces of data from every subgroup.
Evaluating process capability with Cp & Cpk mirrors what is done (and why it is done) when following the Pp & Ppk approach. The main difference is that you use Cp & Cpk after a process has reached stability or statistical control.
Cpk vs. Ppk
Ppk tells us how a process has performed in the past, and you cannot use it to predict the future because the process is not in a state of control.
If a process is under statistical control;
The values for Cpk and Ppk will converge to almost the same value because the sigma and the sample standard deviation will be identical (use an F test to determine).
In other words, if Cpk == Ppk, the process is likely in statistical control.
If a process is NOT in statistical control;
Cpk and Ppk values will differ distinctly, perhaps by a very wide margin.
What is the Difference Between Cp and Cpk?
Cp vs. Cpk
Cp and Cpk measure your consistency compared to your average performance.
The ‘k’ stands for ‘centralizing factor.’ The index considers the fact that your data may not be centered.
Cpk tells us what a process can do in the future, assuming it remains in a state of statistical control.
The Shooting at a Target Analogy
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!In a perfectly centered data set, there will be no difference between Cp and Cpk. Think of throwing darts at a dart board and having the center of the bull’s eye be the 0,0 on a cartesian plane and the edges being out three units from that center point (we will use the edge of the dartboard or 3 and -3 as our USL and LSL). In a perfectly centered sample of darts, your average distance from the center, or Mu, will be 0. A little algebra will show us that your Cpk and Cp numbers are the same. Min((0- -3)/3s , (3-0)/3s) = (3- -3)/6s = 1s .
Things get a little harrier when the darts move up, say to be centered at an average of 2 units above center. Now you end up with a Cpk of (3-2)/3s = 1/3s, but your Cp is still the same 1s as before. It is important to note that because Cpk uses the minimum function, it will always be equal to or smaller than the Cp for the same set of data.
What is Cpk?
The Parking a Car in the Garage Analogy
Think of the walls of your garage – where you have to fit your car – they become the customer specification limits. If you go past those limits, you will crash, and the customer will not be happy!
When your process has a lot of variation, the process average is all over the place. Not good for parking a car or any other process. To give your parking process the best chance of success, you should reduce variation and centering.
If the car is too wide for the garage, nothing you do to center the process will help. You have to change the dispersion of the process (make the car smaller.)
If the car is a lot smaller than the garage, it doesn’t matter if you park it exactly in the middle; it will fit, and you have plenty of room on either side. That’s one of the reasons the Six Sigma philosophy focuses on removing variation in a process.
If you have a process that is in control and with little variation, you should be able to park the car easily within the garage and thus meet customer requirements. Cpk tells you the relationship between the car’s size, the garage’s size, and how far away from the middle of the garage you parked the car.”
How to Calculate Cpk
Cpk is a measure to show how many standard deviations the specification limits are from the center of the process. On some processes, you can do this visually. Others require an equation.
To find Cpk you need to calculate a Z score for the upper specification limit (called Z USL) and a Z score for the lower specification limit (called Z LSL).
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!Since we are trying to measure how many standard deviations fit between the center line and the specification limit, you should not be surprised that the value of those limits, the process mean, and the standard deviation are all components of the Z calculation.
Cp is an abbreviation. There are really two parts, the upper and the lower denoted Cpu and Cpl, respectively. Their equations are:
Cpl = (Process Mean – LSL)/(3*Standard Deviation)
Cpu = (USL – Process Mean)/(3*Standard Deviation)
Cpk is merely the smallest value of the Cpl or Cpu denoted: Cpk= Min (Cpl, Cpu)
Why are we dividing by 3 to find Cpk?
We know that any specification limit has an upper and lower bound. Because you know that 6 sigmas (or six standard deviations account for nearly all eventualities in a process (assuming normal distribution)), you shouldn’t be surprised to see the “/ 3” because we are looking at only one side of the distribution.
Calculating Cpk using a Z Value
If you have a Z value, the equation is very easy;
Cpk can be determined by dividing the Z score by three.
A z score is the same as a standard score; the number of standard deviations above the mean.
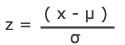
Z = x – mean of the population / standard deviation.
Notes and Characteristics of Cpk
Cpk and Centered Processes
If a process is perfectly centered, it has a Cp of 1. That would indicate that the mean was 3 standard deviations away from the upper limit and the lower limit.
A perfectly centered process is a process that has a mean exactly in between the 2 specification limits (meaning halfway between the two will have a Cpk of 1. How is this possible? Let’s check the math.
If a process is perfectly centered, then we know that the (USL – Process mean) equals the same thing as the (Process Mean – LSL). Let’s call that A.
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!Z USL = USL – Process Mean / Standard Deviation. then becomes Z USL = A/ Standard Deviation
Z LSL = Process Mean – LSL / Standard Deviation then becomes Z LSL = A / Standard Deviation.
The exact same thing.
Notes on Cpk
- Cpk measures how close a process is performing compared to its specification limits and accounting for the natural variability of the process.
- Larger is better. The larger Cpk is, the less likely it is that any item will be outside the specification limits.
- When Cpk is negative, it means that a process will produce output that is outside the customer specification limits.
- When the process’s mean is outside the customer specification limits, the value of Cpk will be negative.
- To satisfy most customers, we generally want a Cpk of at least 1.33 [4 sigmas] or higher.
- Cpk can have an upper and lower value reported.
- If the upper value is 2 and the lower is 1, we say it has been shifted to the left.
- This tells us nothing about whether the process is stable or not.
- We must report the lower of the 2 values.
What are Good Values for Cpk?
Remember the Car parking in the garage analogy?
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!- Cpk = Negative number: Your process will regularly crash the car into the wall.
- Cpk =0.5: You have a good chance of hitting the wall on entry.
- Cpk =1: Your car may be just touching the nearest edge of the entry.
- Cpk =2: Great! You have great clearance. You could double the width of your car before you hit the side of the garage.
- Cpk =3: Excellent! You have excellent clearance. You could triple the width of your car before you hit the side of the garage.
How to Calculate Cp
Just as you use Cp & Cpk when a process is stable and Pp & Ppk when a process is new, the way you calculate each is a bit different, too.
Pp = (USL – LSL) / 6* s
In Pp, s is the standard deviation or the ‘fatness’ or dispersion of the bell curve.
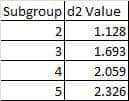
In Cp, we replace s with an estimate of σ we call σr. To do that, we leverage the Moving Range concept from a Moving R Bar chart or an XMR Chart. So, σr = [ R Bar / d2]
R Bar comes from the Moving range.
D2 reflects values derived from integrating the area under the normal curve. We often use a table that gives a d2 value based on how many subgroups were in the sample.
Cp does not account for centering.
First, Cp = (USL – LSL) / ( 6* σr )
Second, Cp = (USL – LSL) / ( 6* R Bar / d2 )
Cp for Process Mean close to USL
If your Process Mean (central tendency) is closer to the USL, use: [ USL – x(bar) ] / [3 * R Bar / d2], where x(bar) is the Process Mean.
Cp for Process Mean close to LSL
If your Process Mean (central tendency) is closer to the LSL, use: [x(bar) – LSL ] / [3 * R Bar / d2], where x(bar) is the Process Mean.
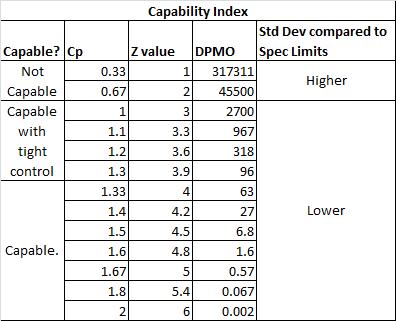
Capability Index
How do Cp, Z values, DPMO, Specification Limits, Standard Deviation, and Capability all relate?
Also, see Z values and process capability.
Notes on Cp Values
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!- If the ratio is greater than one, then the Engineering Tolerance is greater than the Process Spread, so the process has the “potential” to be capable (depending on process centering).
- If the Process Spread is greater than the Engineering Tolerance, then the process variation will not “fit” within the tolerance, and the process will not be capable (even if the process is centered appropriately).
Capability Ratio Cr
The capability ratio is the inverse of Cp
Cr = 1/ Cp = ( 6* σr ) / (USL – LSL)
If Cr < 0.75, the process is capable.
If Cr = 0.75 – 1.00, the process is capable of tight control.
When the Cr >1, the process is not capable.
Notes on Relating Cp And Cpk
- If Cp == Cpk, then the process is perfectly centered. If perfectly centered, Cp == Cpk.
- Because Cpk accounts for centering (where Cp does not), Cpk can never be larger than Cp.
- Both assume a stable process.
Process Capability Videos
Cpk Videos
Great, clear, concise video on this subject.
“If you were producing a Cpk equal to 1, then you could expect to produce at least 99.73% good parts.”
Lecture on Process Capability and SPC
ASQ Six Sigma Black Belt Certification Process Capability Questions:
Question: Data being used in the initial set-up of a process is assumed to have a normal distribution. If the nominal (target) is set at the center of the distribution, and the specification limits are set at ±3s from the center, then the Cpk is equal to:
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!(A) –0.25
(B) 1.00
(C) 1.33
(D) 1.67
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.Upgrade to a Full Membership
If you are a member, you can log in here.
Thank You for being a Member!
Here’s some of the bonus content that is only available to you as a paying member.C: The range of the process is represented by 6 sigmas – or standard deviations in the Cp Index equation. Remember, 6 standard deviations account for nearly all eventualities (assuming normal distribution) of the process. 6 sigmas are a good approximation of the range of outcomes.
The USL – LSL (the upper and lower limits) could be representative of the tolerance interval. I’m not familiar with anything called the tolerance interval, but the upper and lower limits are set by what is considered acceptable by the client. And those fit.
A confidence interval is a statistical measure used in hypothesis testing and is not pertinent to this question.
Variance is a specific term in Six Sigma. You can calculate variance by squaring the standard deviation – a term that does not appear in the Cp equation so we can eliminate this answer.
Cp, Cpk, Pp, Ppk Practice Questions and Z Charts
Practice makes perfect! Free Cp, Cpk, Pp, Ppk practice questions.
Comments (163)
Hi, if I have a set of data where the subgroup size is different, how should I determine which d2 value to be used for the Cpk calculation? If I perform a Ppk calculation, is the Ppk value going to be affected by the difference in subgroup size? Thanks.
Hi Joanna – Not sure I’m following your first question. Are you asking which d2 value to choose if you have multiple subgroups of varying size? (Ex. subgroup 1 has 5 elements, 2 has 4, 3 has 5?)
However, Ppk values shouldn’t be affected by subgroup size as you don’t use it in the calculation. – See this article on Ppk calculation.
Yes. My first question was about how to determine d2 for multiple subgroups of varying size, i.e. what you have given in the example.
Joanna, you’ve asked a great question and I’m going to need to study a bit more before I can answer.
If you were designing the sampling, I’d suggest controlling it so that your subgroups were the same size. Since we all know that in practice we often inherit data, so this may not be possible. My instinct would be to take the average of the subgroup sizes. So if we had sizes of 5, 4, 5 – I’d round up and use 5.
I’ll investigate further and see what I find. A friend suggested I check the text Statistical Quality Control by Grant and Leavenworth. Trying to get my hands on a copy now.
Hi, I am doing data analysis where the subgroup size is not constant. I was thinking to take the majority (or average) but I have found that there is formula to determine the sigma. Have a look here: http://elsmar.com/pdf_files/Capability%20Analysis%20Formulas%20-%20Minitab.pdf
Hi, can be Cp=4.395
Cpk=1.688
Use S bar / C4 instead of r bar /d2. C4 is a different form of unbiasing constant that doesn’t require the sub groups to be the same size.
WHAT IS DIFFERENCE between CP and CPK?
The Shooting at a Target Analogy
A good analogy is shooting at a target. If the rounds form a good cluster or grouping in the same spot anywhere on the target you have a high Cp value. When the you have a tight group of shots is landing on the bulls eye, you now have a high Cpk
Cpk measures how close you are to your target and how consistent you are to around your average performance. A person may be performing with minimum variation, but he can be away from his target towards one of the specification limit, which indicates lower Cpk, whereas Cp will be high. On the other hand, a person may be on average exactly at the target, but the variation in performance is high (but still lower than the tolerance band (i.e., specification interval). In such case also Cpk will be lower, but Cp will be high. Cpk will be higher only when you r meeting the target consistently with minimum variation
Hello! How was out of spec percentage (2.28%) calculated in a video lesson?
Hi Pavel, it was calculated using a Z Score. See some more on the relationship between Process Capability and Z scores here: https://sixsigmastudyguide.com/z-score-and-process-capability/
Then, see how to do the equation by following the examples here: https://sixsigmastudyguide.com/z-scores-z-table-z-transformations/
Can we calculate Cp & Cpk for components batch size of 2 or 3.
Yes, Parag. See the notes that Joanna Han left above.
process capability studies
Abdul – not exactly sure what you’re looking for here. How can I help?
cpk value is 1.12 , is it process is good?
It’s ok. It’s not great.
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
best summarized Cp Pp Cpk PPk chart that capsulizes dignificant facotrs
No idea what you are asking for.
what is guide lines (which)for process capability limit in Pharmaceutical industreies
What is the value of Cpk for six sigma process
It’s an equation, Abhinav. Read the article.
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
A process that has a Cp ≥ 1 and a Cpk ≤ 1, is
What do you think, Prabin?
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Can you solve the problem?
The weights of nominal 1-kg containers of a concentrated chemical ingredient are shown in Table 8E.2. Suppose there is a lower specification at 0.995 kg. Calculate an appropriate process capability ratio for this material. What percentage of the packages produced by this process is estimated to be below the specification limit?
weights of containers
0,9475 0,9775 0,9965 1,0075 1,018
0,9705 0,986 0,9975 1,01 1,02
0,977 0,996 1,005 1,0175 1,025
Yes, I can. What have you tried so far?
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
How many number of batches Require for caculation of Cp & CPk Valules in Anual product quality review
Hi Chandana, What do you think would be appropriate and why?
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Hi,
I have a doubt about the table under the “Capability Index” paragraph. It links Cp and Z, and there is a constant Cp=Z/3. My question is should not be Cpk=Z/3?, instead for Cp should be Cp=Z/6. Thanks in advance
Hi Gianfranco, Why should it be Cp = Z/6? Where do you see that?
Hello,
I would like to know more whether we can calculate process capability of Manual processes & what are the rules to calculate manual process capability (Theory).
Thank you so much.
Hi Amit,
I’ve added videos to help explain. Do they help?
Best, Ted.
Hi,
1.How much OK ratio there is in Cp=1.33 and Cpk=1.33?
2.How much OK ratio there is in Cp=1.0 and Cpk=1.0?
Thank you
Erica, I’m not sure what you mean by OK ratio. Can you elaborate?
Hi,
I have a data which contains the quality scores of the individual persons from last 50 weeks (Individual scores for 50 persons on 50 weeks).
Can I use the cpk calculation to know how many persons are in USL & LSL?
Or any other method will be used ?
Please suggest. Thanks in advance.
Guru, I’m not entirely sure what you are asking. Can you add a bit more detail?
Hi,
Sorry for my unclear question before.
Currently, I have been measuring the quality for a group of staffs on a weekly basis. I also set a bandwidth that the staffs who scored more than 90 percentage were good and less than 90% was bad.
Now I have the data history for the last one year. If I want to see the statistical detail for the past one year data(which means can I able to say the sigma levels for each staff) what method will be used?
Interesting question. Is the sample size homogeneous? Were the same people measured for every test or did the population change over time? Was the test the same each time?
Thanks for the comments.
1.The sample size was homogeneous.
2.Mostly same people were measured for every test. Sometimes, the new people were added and will be added overtime.
3.The population will slightly change every time.
4.The testing method will be the same each time.
Hard for me to give a straight answer without knowing more details on what kind of analysis you will be looking to do, but here are some thoughts:
Since this looks like attribute data (pass / fail), consider treating it like so and forget the scores. Then use an attribute chart to show changes over time where each fail is a “defective” not a “defect”. You’d calculate baseline sigma like so.
Look at what Jeremy did in his case study on using control charts on student test scores. Depending on your use, you might consider an EWMA chart.
If you want to compare the different populations against each other, consider a MANOVA.
Hi
Thanks very much for the detailed response.
Now I will start my analysis with the baseline sigma.
However, I will consider the other sources for my future analysis plan
Thanks again
How does a Cpk of 2.0 translate into 6 sigma
quality?
• Must show the calculations supporting your response.
This is a good homework question because it shows the relationship between process capability and quality. Start by listing the Cpk formula and substituting the 2.0 value. What are you left with?
It is a homework question. I put CPK=Z/3=6/3=2 and he said it wasnt good enough. He said, define the Cpk and Z score formulas first.
Then start applying your substitutions. Begin with the given, i.e. Cpk = 2.0.
From there, see how to elegantly interconnect the Z score in the Cpk formula.
I see. Try this walkthrough on z score and process capability.
Dear Sir, I wish to sign up to your newsletter. Thanks a lot!
Hi Adam – we’d love to have you!
The best place is to sign up here.
You’ll get access to a bunch of free questions, lots of help answering them, as well as practice tests, strategies, and other helpful downloads.
pls how do you solve this -What is the Ppk of a process with a spread of 24 units, an average of 68, an upper limit of 82 and a lower limit of 54
Alex, what have you tried here?
I have the same question when preparing for ICBB – all solutions do not make sense.
My calculation Ppk = 14/(24*3)
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
In the section “How to Calculate Cpk” you describe Cpk as the minimum of two scaled z-scores, where those scores are Cpl and Cpu (the “Cps”). Z-scores are calculated using standard deviations, which you also say in that section and immediately following ones. But later on in the “How to Calculate Cp” section you say that you don’t use standard deviation, instead you use the range: R_bar / d2.
Which is it?
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Req dimension 49 , tol+/- 1, capture value all of them within48.9 to 49.2 but cp value comes around 0.3 , even all the data are close to required value why cp is less than 1? Captured 125 data,n 5
Sabarish, can you show your calculation here?
All dimensions are in mm
Great excel sheets here:
http://www.cpkinfo.com/CapStudy.html
hi
i want to calculate the cp and cpk for a group of data =250 value and the subgroup of them is 1 .(every data of the 250 value is a subgroup itself)
how can i do that
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
When cpk and ppk are close in value it represents a stable process, and when they are far apart it shows an unstable process. My question is, how far apart can they be where one can say if the process is stable or unstable.
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
I m involved in manufacturing of pharma products.Total number batches are 10 and Cpk of assay of batches is 0.97. Is it acceptable ?? If not then what would be the imapct of sample size on Cpk ?? Please reply.
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Hi Ted:
I appreciate that you continue share the six sigma information to me. We have some questions about six sigma calculation.
I think that I can discuss with you , could you please kindly to answer?
1. When we talking about the capability of a process , we usually use cpk to show how well the process is.
For example , if a dimension is a key characteristic of a product , we have USL and LSL from the drawing.
We want to know the capability of the process . So we sample 32x and we can calculate the cpk of the dimension from the 32x data.
Besides , according to the ‘Central Limit Theorem’ , we can easily calculate the estimated failure rate. (normal probability. )
And we can transfer cpk to sigma level because
But how about a attribute data? If I know the yield rate of our product (like 95% ), how can I transfer 95% to a sigma value?
In general case , we often say that the yield is 95% and maybe sigma level Z= XXXX , do you know what is their relationship?
And if we can transfer yield to sigma level . Do we need to measure the process drift(according to Motorola , the long term drift is 1.5 sigma)? Or we just need to calculate the short term sigma level?
Hi Ted:
I appreciate that you continue share the six sigma information to me. We have some questions about six sigma calculation.
I think that I can discuss with you , could you please kindly to answer?
1. When we talking about the capability of a process , we usually use cpk to show how well the process is.
For example , if a dimension is a key characteristic of a product , we have USL and LSL from the drawing.
We want to know the capability of the process . So we sample 32x and we can calculate the cpk of the dimension from the 32x data.
Besides , according to the ‘Central Limit Theorem’ , we can easily calculate the estimated failure rate. (normal probability. )
And we can transfer cpk to sigma level because
But how about a attribute data? If I know the yield rate of our product (like 95% ), how can I transfer 95% to a sigma value?
In general case , we often say that the yield is 95% and maybe sigma level Z= XXXX , do you know what is their relationship?
And if we can transfer yield to sigma level . Do we need to measure the process drift(according to Motorola , the long term drift is 1.5 sigma)? Or we just need to calculate the short term sigma level?
Wisely, That’s great question that will take a lot of thought.
At first pass I think you can examine the relationship between z scores and process capability here.
Perhaps I’m missing something, but I don’t think you would account for process drift on something you just sampled. Am I interpreting your question correctly?
Best, Ted
There appears to be a mistake in the material on this page…
Here is the statement, from the Shooting at a Target Analogy:
“On the other hand, a person may be on average exactly at the target, but the variation in performance is high (but still lower than the tolerance band (i.e., specification interval). In such case also Cpk will be lower, but Cp will be high. Cpk will be higher only when you r meeting the target consistently with minimum variation”
The issue is that, if we are perfectly centered, the Cp = Cpk, which is not what the penultimate sentence says. The final sentence also implies that Cpk can be higher than Cp, which is not true.
This is a good question. I’ve added this to my list of improvements. Stay tuned…
This section is also wrong…
“Notes and Characteristics of Cpk
Cpk and Centered Processes
If a process is perfectly centered, it has a Cp of 1. That would indicate that mean was 3 standard deviations away from the upper limit and the lower limit.
A perfectly centered process – a process who has a mean exactly in between the 2 specification limits (meaning halfway between the two will have a Cpk of 1. How is this possible? Let’s check the math.”
Cp has nothing to do with whether a process is centered. There is no sample mean in the equation! Cp is the ratio of the spec range over the sample std dev. Cp = 1 when they are equal, and can be far greater than 1. Cpk is also =/= 1 just because the process is perfectly centered. In that case, Cpk = Cp.
Again, this is a good question. I’ve added this to my list of improvements. Stay tuned…
In the framework of process evaluation and analysis, CP and CPK are used as indicators of processes, but as I seen,
they are more oriented towards each metric in particular than the process as a whole, for example, I have a human talent management process,
that has three metrics, you can calculate the CP based on the specification limits of each metric, the standard deviations of those
The data, but how would the roll-up or grouping of information to measure the capacity of the human talent management process like everything?
Thanks
Hi Dany,
I only have the capacity to answer these kind of questions in the paid forum. We’d love to have you join!
Best, Ted.
I am a QHSE mgr, in an industrial company for prefabricated substations and switch-gears and control panels,it means we’re not a mass production company and the only one product may has a many defects .
how to calculate the CP for the assembly processes and other processes.
thank you
Hi Samy,
This is a great question. Right now I only have the capacity to answer these kind of questions in the paid forum. I’d love to have you join!
Best, Ted.
Using this partial Z Table, how many units from a month’s production run are expected to not satisfy customer requirements for the following process? Upper specification limit: 8.4 Lower specification limit: 4.7 Mean of the process: 6.2 Standard Deviation: 2.2 Monthly production: 360 units
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Application for Copyright Permission For Educational Use
November 29, 2018
The Southern Regional Education Board (SREB) and the state of Ohio are partnering in the development of an Automated Materials Joining Technology (AMJT) curriculum for high school students. The curriculum is part of SREB’s Advanced Career (AC) project that involves 9 states in the development of project-based curriculum with each state authoring its own unique career area.
We are writing to request copyright permission for teachers and students to view the following link for completing Project 2 in Course 3 (Advanced Concepts in Materials Joining):
https://sixsigmastudyguide.com/process-capability-cp-cpk/
Also, no changes in or deletion of author attribution, trademark, legend, or copyright notice will be made, if permission is granted.
We hope you will be able to respond positively to our request.
We will cite appropriately.
Thanks.
Jim Berto
James J. Berto
AC Program Manager/Research Associate, School Improvement
Southern Regional Education Board
592 Tenth Street, N. W.
Atlanta, GA 30318-5776
Phone 404-875-9211, ext. 228
Direct 404-879-5528
Fax 404-872-1477
james.berto@sreb.org
http://www.sreb.org
I want to calculate the Cpk of a set of data where the target is offset from zero. Is the Cpk equation need to be modified to include this offset target? And what is the new Cpk equation?
Hello, Can you tell me if we can calculate percentage non defectives using the values of Cp and Cpk?
Greeshma,
Yes, I can tell you, but let’s reason it out together.
Look at the equation for Cp and the equation for Cpk -do you see any values there that could help us calculate defective rate?
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Hi! Can you use Cpk in any experiment given that the data follows a normal distribution? I am currently dealing with mixture designs.
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Hi Ted. Really helpful, but I think I am getting confused with Ppk, Pp, Cpk and Cp. Someone asked a question a while ago but I could not see it answered and I have had the same question in a mock that I cannot work out why the answer is as is is supposed to be. The question is:
What is the Ppk of a process with a spread of 24 units, an average of 68, an upper limit of 82 and a lower limit of 54?
Options are 2.00, 1.68, 4.42 or 4.00. I get 1.17 using min[(82-68)/(24/2) ; (68-54)/(24/2)]
Any idea why the idea is supposed to be 4.00? Some sites suggests the question is incomplete, but I think it is complete, just incorrect options and answer. Help appreciated thanks so much!
Hi Naomi. I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Can Cpk be calculated for a manufacturing process before the part has even entered the sample stage? I am attempting to fill out a feasibility commitment for a product that has not been made before.
I’m not sure, Avery. Let me see if I understand what you are asking.
You are looking to predict the future Cpk of the process? If so, how are you going to determine the standard deviation?
For a certain process, Cp=0.93 and Cpk=0.93. What action you likely to take?
Reduce the variation
Address either the mean or the variation
Move the mean
Move the mean and reduce the variation
Thanks for the question! I’ve added this as a question in the Pass Your Six Sigma Green Belt question set. Sign up or log in for access.
Hi Ted,
My current CPK value oscilatted between 1.37 to 1.88 cpk
how I can improve and stabilize above 2 cpk.
my process – nut tightening process (we measure here torque)
action taken – incase the cpk come under 1.33, I reduce the speed and it will go above 1.33
but I cannot reach the value to 2.
please reply
I would like to know what is Prediction interval and Tolerance interval? what are they use for?
How is CP, CPk (within) curve calculate? what is the connection between their number and our machinery?
Hi Hasti,
What have you tried so far?
I am working with them and need to know
can you please give me an example on how to calculate a CPK for attributes in a mfg process
There are several examples above, Rafa. Can you be more explicit with your request?
Hi, first of all: thanks for the article!
I have problems in calculating the Cpk/ Ppk for a special case:
– My specification limits are: 1600 – 1800.
– The historical mean is around 1790 with a low standard deviation of 2.
This is because the aim is to produce as close as possibble to the upper spec. limit.
If I use now the defined specifiation limits, I always get Ppk below 1.
So far, I tried the following:
– used control limits only; but Ppk is still below 1 because the process is close to the target.
– used USL as the natural boundary. Then Ppk equals PPL and is above 1.33 because the process is far away from the lower spec. limit. However, this is not realistic and with this case, I I can not control the upper limit…
– used historical values (within stdev and mean); still Ppk below 1.
Do you have an advice?
Best,
Laelia
Insert 1780 as your LSL.
USL 1800. If you really want to target the Upper specification Limit and your current process is where you want it to reside.
By centering your Mean to be on Target you have today Disregard the fact the USL is a full 190 points away from your Mean.
As you stated your Sigma is low 2.0 .
Instead of showing, or calculating your process to show you are extremely Skewed (95 Sigma away from your Lower Specification Limit) and only 5 Sigma from your Upper Specification limit. Just know you have a tremendous safety buffer on the Lower end of your specification. One has to ask Why do you want to target the Upper specification 1800 instead of 1700?
Hi Mike,
Thanks for answering!! ( I think you meant percent instead of sigma in your last paragraph though)
Hi Lealia,
Mike has some excellent thoughts here. In short, if you are incentivized to be as close as possible to the Upper Spec Limit, a tool that measures centering is going to be of limited use.
Mike’s approach to disregard the 1600 LSL and instead use your process mean is interesting. It will certainly help force the equation. I might argue using a full deviation less than the process mean as an LSL but I think Mike has far more practical knowledge than I here!
My fundamental question is one around effectiveness vs efficiency. It feels like chasing the USL favors efficiency over effectiveness.
My advice would be to first reduce variation (ie improve from 2 sigma) before worrying about getting as close as possible to the USL.
Not doing so gives you a good chance of never actually acheiving effectiveness, as demonstrated in this Quincunx video here.
Hello Ted,
First at all, thank you for the explanation. It was a good way to explain all these terms. I hope you can help to clarify these doubt. For the developing the subcomponents of our product, we used to define some dimensions with “K” (key functional characteristic >1.33 Cpk) ). I’ve read that key characteristic is a deviation within tolerance, but my colleagues consider it for a deviations out of the tolerance. What would be correct?
BR
Williams
Hi William,
Thank you for the question. To be honest, I’ve never encountered that term. However, I was able to find the following:
SAE – Society of Automotive Engineers – defines Key Characteristics as follows:
MIT’s open course on Mechanical engineering defines Key functional characteristics as:
My interpretation of what I’m reading agrees with yours – this is variation within tolerance.
Hello Ted,
Thank you so much for the clarification! I’ve learned a lot These last days reading you blog 🙂
I wish you a nice day!
Best regards
Ted,
If I run 30 pieces through a new process can I get an accurate CpK and will this tell me if the process is capable the next time I run 3000 pieces?
Or is it best to randomly select pieces throughout the 3000 pieces or pick the first 30 pieces from the run of 3000?
Thanks
Al Morrison
Hi Sir
Lot of good information in the article. I needed some clarity on whether I had to do complete process capability studies or a simple process performance would do during PPAP. Your article sheds good info on that.
Thank you
Glad it helped, Krishna!
What about the scenario where there’s a USL but no LSL? Say I am measuring torque on a part (how much twisting force for it to turn), and the USL is 100 oz-in but the less the better. If it only takes 10 oz-in to turn it, great; we’re way below the spec. The LSL is technically zero I guess because it physically doesn’t make sense for the measurement to be less than that. But then the Cpk is taking the lower of the two Cp values. Should a super low number be put in for LSL (-999999) to make it to where Cpu>Cpl and Cpk is more meaningful?
*** Cpu<Cpl
That’s an interesting scenario that I’ve never encountered!
I’m inclined to agree with the writer of this article about Calculating capability indices with one specification; “Since you do not have a LSL, Zlower is missing or non-existent. Zmin therefore becomes Zupper and Cpk is Zupper/3.”
Thanks for the reply! I am also inclined to agree with that article. And their example is exactly like what I’m currently dealing with. The SPC software that we use is Proficient by InfinityQS, and so far as I’ve seen, it won’t even calculate a Cpk unless all values are present (Xbar, sigma, USL, LSL). Which is unfortunate. At any rate, thanks again!
Hi , Can anyone explain this question. (Answer is 12)
if 6sigma spread for a process is 6, and process average is 16 ,what should be lower spec limit be set to ensure less than .135% of the process output is rejected.
Hi , Ted if u can help for this question?
Hi Nabeel,
I’ve moved this to the member’s forum.
Best, Ted.
Hi , Ted if u can help for this question?
Hii sir, let consider below situation.
Am having maximum material condition tolerance for hole position, So specifications changes depends on part size. This condition how to calculate process capability (cp & cpk)?
I would suggest that creating a part of a specific size is one process. Sounds like you’re putting too many processes together.
Hi All,
I have two questions on a practice test I’m having trouble answering.
Thanks!
Hi Jennifer,
I moved the question to the member-only thread here and should be able to work it shortly.
Please post any questions there and away from the public pages.
Thanks, Ted.
Ok, no problem. Thanks!
Hi
What is different between natural tolerance and standard deviation?
are both formula are same?
– Cpk Upper = USL – Mean / 1/2 of natural tolerance
– Cpk upper = USL – Mean / 3* standard deviation
Wide range of specification limit is impacted on ppk value ? If it is what is reason ?
Hi,
I prepare the BB IASSC certification. You can send me the article even better for me, as you propose.
Thanks a lot.
Hi Katia,
This is already available inside the member’s area. I’ll catch up with you over email.
Best, Ted.
Hi,
We are a resin compounder. We buy prime or recycled resin as a raw material and add modifiers/colorants to produce custom resins for injection molders. We have a new customer that that molds automotive parts from our resin. They want us to provide Cpk data on our compounding process. Our process is one of discrete batches. For example, we have a blender that holds 5000# of a resin recipe. We compound a small amount of the batch and perform property testing on it. If it tests in spec, we run out the batch. If it needs a recipe adjustment for a certain tested property, then we make the adjustment and repeat the process. What we end up with over time is a collection of lot data that is always in-spec but scattered all over the place because when a batch is in-spec we run it out (whether centered or just barely in). Also, our lots for this resin run only four or five times a year. Can we make a case that our bulk material process of discrete batches is just not suited to the type of Cpk statistical analysis they want? Thanks, ME
Hey Ted. I think these two terms have been switched. PP and PPk are used for long term data. For reference, see https://www.six-sigma-material.com/Cpk.html.
“Cp, and Cpk are used for Process Capability. Generally you use this when a process is under statistical control. This often happens with a mature process that has been around for a while. Process capability uses the process sigma value determined from either the Moving Range, Range or Sigma control charts
Pp and PPk are used for Process Performance. Generally you use this when a process is too new to determine if it is under statistical control. Ex. there is a short pre-production run or you are piloting a new process. Because there is not a lot of historical data we take large samples from the process to account for variation. Process Performance generally uses sample sigma in its calculation.”
Hi Ted,
I have learned that you should calculate Cp and Cpk when your process is stable and take a production run of 30 parts without making any adjustments to the machine. I am working with a CNC machine and wish to calculate its capability to hold the tolerance. But, with every part produced, the dimension goes down because of the tool wear and I cannot make a run of 30 parts without making adjustments. How can I calculate Cp or Cpk in this scenario?
It doesn’t sound like the process is stable then.
Hi , I need help on understanding the symbol & before a dimension in thedrawing. Is this related to SPC?
Hi,
Please, who can tell me how to find the constant “d2” for samples size exceeds 5 (30 samples for example). Table, an empirical function?
Another point, “d” depends on the number of measurements for the subgroup or number of subgroups. in several references, I find that it represents the number of measures by the subgroup
Thank you
Bessem,
We have a few resources on data sampling techniques and sample size here.
Best, Ted.
may i know wht is the relation between sixsigma tabulated values in ppm to cp&pp
Hi Sathesh,
Thank you for the question.
See the article here.
Best, Ted.
Hi, I have a specification, which sets 6 limits for a production process.
1-each measurement less than 6.5 then Acceptable
2-each measurement 6.6 to 7.5 then Borderline
3-each measurement greater than 7.6 then Rejectable
4-average of 4 measurement less than 5 then Acceptable
5-average of 4 measurement 5.1 to 6.5 then Borderline
6-average of 4 measurement greater than 6.6 then Rejectable
I am asked to make control chart for individual measurements and range. I have no problem for creating individual measurements control chart, but cannot figure out how to find my upper and lower limits for range chart based on the above conditions.
I’m studying for the Lean Six Sigma Yellow Belt
Great, Franz – how can I best help?
Hi Ted. I have a manager asking me to provide CPk data for a special design characteristic feature. We typically do not use CPk to track these, because our processes require that we measure every part and document our results. Special design characteristics have a very small tolerance band, thus the CPk value will be naturally low. The parts are pass/fail depending upon the measurement results, and some scrap is expected. Am I thinking about this correctly? And if so, can you give any advice on how I can simply explain to this manager why his request is unreasonable? Thanks
if we have
Cp=1
Cpk=0.78
then what is process actual capability.
??????
What have you tried so far, BJ?
Best, Ted.
Hi Ted. Let’s say i have 30 parts to run for getting the CPK data. In the middle of the process, one of my parts was failed the result, 1/30 part. So i need to adjust the machine as to ensure the part result pass (assuming there have machine issue). Do i need to remeasure all those 29 parts after adjusting the machine?
Azim,
If you change the process (ie adjust the machine), you have a completely new process.
Take a look at this quincunx demonstration and you’ll understand why.
Best, Ted.
Can Cp/Cpk be like around 10-20 range?
Well, let’s look at the math.
Cpl = (Process Mean – LSL)/(3*Standard Deviation)
Cpu = (USL – Process Mean)/(3*Standard Deviation)
Cpk is merely the smallest value of the Cpl or Cpu denoted: Cpk= Min (Cpl, Cpu)
Can you construct a scenario where you would get a Cpk in that range?
@Ted Hessing, Could you pls share more insights into the statement where it say if Cpk= Ppk, the process is under statistical control.
Gaurave,
Did you see the paragraph before that statement?
What can I clarify here?
Best, Ted.
I want to assess the impact on Cp when I chop a tail of a distribution which is normal to begin with. If you have a ready reference please let me know.
I am thinking of the following: say we have normal distribution data with a given sigma and mean.
Now I want to see if I remove the lower 10th percentile and the top 90th percentile of the data what will happen to my cp and cpk.
I am thinking of the following approach
1. Knowing 10 and 90th percentile work through the z value and come up with the corresponding x values for these percentiles
2. Make these new x values as the new say 6 sigma values and compute the new sigma – this is trivial but it is a step
3. Compute the new cp and cpk using the same mean but new sigma.
The question is: is there a mathematical formulation that you can point to vs doing this manual operation. Is this approach valid or there are other approaches?
If you remove the tails, do you still have the same mean?
which parameter can be consider for calculating Cp and CpK value for parenteral from below,
pH
Colour index
Assay
weight per ml
particales
I’m not sure I understand your question, Amit. What do you mean by Parental?
How many number of batches Require for caculation of Cp & CPk Valules in Anual product quality review
Well, in what cases do you need multiple batches?
What kind of data are you processing?
1. Cpk is a process capability index that measures how close a process is running to its specification limits [(Upper specification Limit(USL) and Lower Specification Limit (LSL)], relative to the natural variability of the process. It evaluates how well the data fits into the specification limits. A comparison is made by forming the ratio of the spread between the sample mean and process/ product specifications, as measured by 3 standard deviation (std.Dev.) units (the process”width”).
Cpk= Process Capability Index
USL= Upper Specification Limit
LSL= Lower Specification Limit
µ= Mean (Average)
σ=Standard Deviation
Cpk= Min. [(USL- µ)/3 σ, (µ-LSL)/3 σ]
Or
Cpu= (USL- µ)/3 σ
Cpl= µ-LSL)/3 σ
Cpk= Minimum of {Cpu & Cpl}
2. A Cpk≥1.33 is desirable, a value of Cpk=0 implies that 50% of the process output falls beyond the specification limits. The larger the index, the less likely it is that any parameter will be outside the specification.
3. If Cpk is between 1 and 1.33, site may review to improve the product process. Evaluate if any repeated OOS/OOT results are being logged. Evaluate all changes pertaining to manufacturing and analytical processes. Detailed assessment shall be performed to identify the actions to improve the Cpk.
4. If Cpk is less than 1, action shall be taken to review and correct the product process.
i need guideline of above information
What kind of guideline are you looking for?
Hi, can be Cp=4.395
Cpk=1.688
Usl =42,4
Lsl =42
6s=0.091
If question is asking us to evaluate the process capability. Do we need to calculate Pp & Ppk as well in addition to Cp & Cpk?
Hi Dora,
I can only comment on the problem sets within my program. Why not join up and ask away?
Best, Ted.
Hello! cpkgo.com is a cpk generator, it is very helpful to explain and understand what a cpk is linked to in minitab
https://www.youtube.com/watch?v=Akdq-fYymws
Hi ted
what to do if CPK calculation get fail ? if it found below 1.33
Larger is better. The larger Cpk is, the less likely any item will be outside the specification limits.
Sounds like you should take action to look for common cause variation, address that, and then re-check the capability to see if you’ve increased the stability of your process.
Hi, It is really good for understanding, do you have any excel template, of Cp, Cpk which can automatically create Histogram, Conntrol chart, after putting values
I do not, Karunesh. But that is a good suggestion.