Statistical Process Control (SPC) is a statistical method to measure, monitor, and control a process. It is a scientific visual method to monitor, control, and improve the process by eliminating special cause variations in a process.
History of Statistical Process Control (SPC)
SPC has been used in Western industries since 1980, but it started in America’s twenties. Walter A. Shewhart developed the control chart and the concept that a process could be in statistical control in 1924 at Bell Telephone Laboratories, USA. Likewise, the SPC concepts were included in the management philosophy by Dr. W.E. Deming just before World War II. However, SPC became famous after Japanese industries implemented the concepts to compete with Western industries.
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!Meaning of SPC
- Statistics: Statistics is a science that deals with the collection, summarization, analysis, and drawing of information from the data.
- Process: It converts input resources into the desired output (goods or services) with a combination of people, materials, methods, and machines, as well as measurements.
- Control: System, policies, and procedures in place so the overall output meets the requirement.
Why use Statistical Process Control
Today companies face increasing competition and operational costs, including raw materials increasing. So, it is beneficial for organizations to have control over their operation.
Organizations must try to continuously improve quality, efficiency, and cost reduction. Many organizations still follow inspection after production for quality-related issues.
SPC helps companies move towards prevention-based quality control instead of detection-based quality controls. By monitoring SPC graphs, organizations can easily predict the behavior of the process.
Statistical Process Control Benefits
- Reduce scrap and rework
- Increase productivity
- Improve overall quality
- Match process capability to product requirement
- Continuously monitor processes to maintain control
- Provide data to support decision-making
- Streamline the process
- Increase in product reliability
- Opportunity for company-wide improvements
Statistical Process Control Objective
SPC focuses on optimizing continuous improvement by using statistical tools to analyze data, make inferences about process behavior, and then make appropriate decisions.
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!The basic assumption of SPC is that all processes are generally subject to variation. To that end, Variation measures how data are spread around the central tendency. Moreover, variation may be classified as one of two types, random or chance cause variation and assignable cause variation.
Common Cause: A cause of variation in the process is due to chance but not assignable to any factor. It is the variation that is inherent in the process. Likewise, a process under the influence of a common cause will always be stable and predictable.
Assignable Cause: It is also known as “special cause.” Therefore, the variation in a process that is not due to chance can be identified and eliminated. In this case, a process under the influence of a special cause will not be stable and predictable.
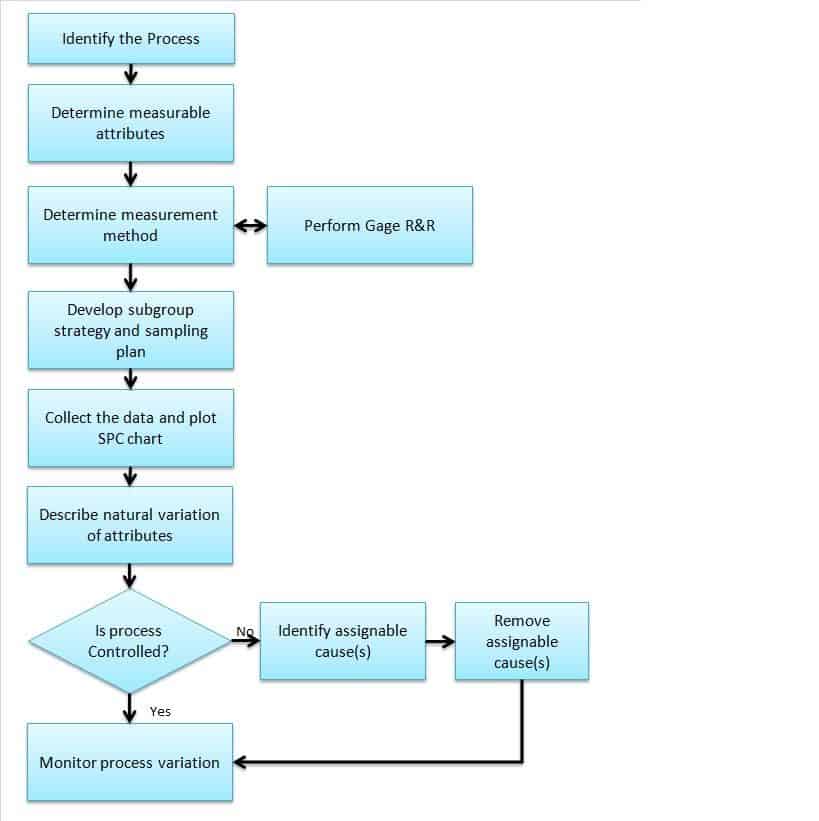
How to Perform SPC
1. Identify the processes:
Firstly, identify the key process that impacts the output of the product or the process that is very critical to the customer. For example, plate thickness impacts the product’s performance in a manufacturing company, then consider the plate manufacturing process.
2. Determine measurable attributes of the process:
Secondly, identify the attributes that need to be measured during production. For example, consider the plate thickness as a measurable attribute.
3. Determine the measurement method and also perform Gage R&R:
Thirdly, create a measurement method work instructions or procedure, including the measuring instrument. For example, consider a thickness gauge to measure the thickness and create an appropriate measuring procedure. Perform Gage Repeatability and Reproducibility (Gage R & R) to define the amount of variation in the measurement data due to the measurement system.
4. Develop a subgroup strategy and sampling plan:
Fourthly, determine the subgroup size based on the product’s criticality and determine the sampling size and frequency. For example, collect 20 sets of plate thicknesses in a time sequence with a subgroup size of 4.
5. Collect the data and plot the SPC chart:
Then, collect the data per sample size and select an appropriate SPC chart based on data type (Continuous or Discrete) and subgroup size. For Example, for plate thicknesses with a subgroup size of 4, select Xbar -R chart.
6. Describe the natural variation of attributes:
Next, calculate the control limits. From the above example, calculate the upper control limit (UCL) and lower control limit (LCL) for both Xbar Ranges.
7. Monitor process variation:
Finally, interpret the control chart and check whether any point is out of control and the pattern.
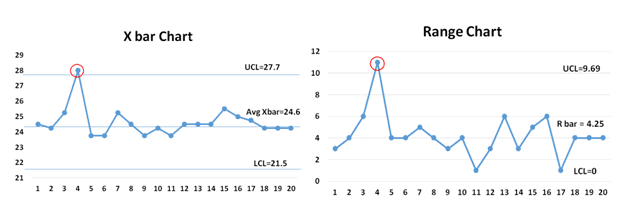
Example: Check the Xbar R chart if the process is not in control, then identify the assignable cause(s) and address the issue. This is an ongoing process, so monitor the process variation.
Additional Statistical Process Control Resources
Control limits are the voice of the process (different from specification limits, which are the customer’s voice.) They show what the process is doing and act as a guide for what it should be doing. Control limits also indicate that a process event or measurement is likely to fall within that limit.
Control charts: A Control chart is one of the primary statistical process control techniques (SPC). The control chart is a graphical display of quality characteristics that are measured or computed from a sample versus the sample number or time. Furthermore, the control chart contains a center line that represents the average value of the quality characteristics and two other horizontal lines known as the upper control limit (UCL) and lower control limit (LCL)
The selection of an appropriate control chart is very important in control chart mapping. Otherwise, it ends up with inaccurate control limits for the data. The control chart selection depends on the data type: Continuous or Discrete.
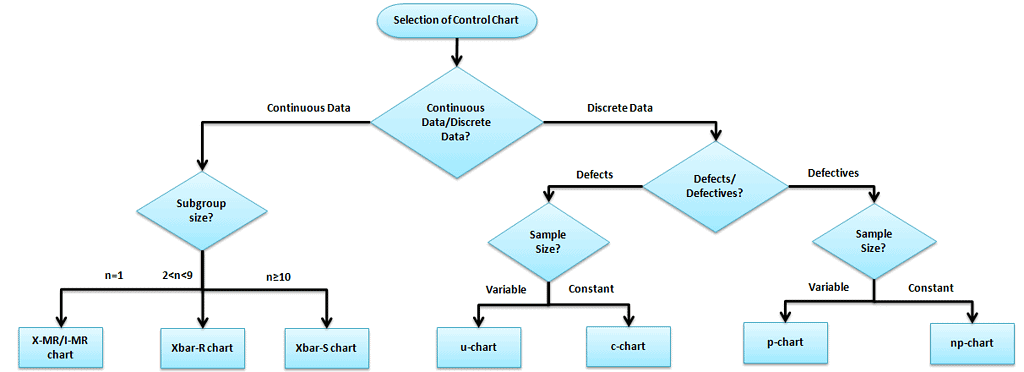
Variable (Continuous) Control Charts
Measure the output on a continuous scale. It is possible to measure the quality characteristics of a product.
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!X bar – R Charts (when data is readily available)
- X bar R chart is used to monitor the process performance of continuous data and the data to be collected in subgroups at set periods. In other words, two plots monitor the process mean and the process variation over time.
Run Charts (limited single-point data)
- A run chart displays observed data as they evolve over time. Just a basic graph that displays data values in a time order. It can be useful for identifying trends or shifts in the process but also allows you to test for randomness in the process.
X – MR Charts (I – MR, individual moving range)
- An I-MR chart is also known as an X-MR chart. An Individual moving range (I-MR ) chart is used when continuous data is not collected in subgroups. In other words, collect a single observation at a time. An I-MR chart provides process variation over time in a graphical method.
X bar – S Charts (when Sigma is readily available)
- X Bar S charts often used control charts to examine the process mean and standard deviation over time. These charts are used when the subgroups have large sample sizes, and the S chart provides a better understanding of the spread of subgroup data than the range.
EWMA Chart
- The EWMA – Exponentially Weighted Moving Average chart is used in statistical process control to monitor variables (or attributes that act like variables). Additionally, it makes use of the entire history of a given output. This differs from other control charts that treat each data point individually.
Attribute(Discrete) Control Charts:
The output is a decision or counting. It is not possible to measure the quality characteristics of a product. In other words, it is based on the visual inspection like good or bad, fail or pass, accept or reject.
- p Charts: (for defectives – sample size varies) – Use P chart when the data are the fraction defective of some set of the process output. It may also be shown as a percentage of defective. The points plotted on the p-chart are the fraction of non-confirming units or defective pieces found in n samples.
- np Charts (for defectives – sample size fixed) – Use an np-chart when the data is collected in subgroups that are the same size. Np-charts show how the process changes over time, measured by the number of nonconforming items (defectives) produced. In other words, the process describes pass or fail, yes or no.
- c Charts (for defects – sample size fixed) – Use c charts when the data are concerned with the number of defects in a product. The number of defects collected for the area of opportunity in each subgroup.
- u Charts (for defects – sample size varies) – A u chart is an attribute control chart that displays how the frequency of defects or nonconformities changes over time for a process or system. The number of defects collected for the area of opportunity in each subgroup.
Statistical Process Control Links
Great decision matrix here: https://www.moresteam.com/toolbox/statistical-process-control-spc.cfm
Statistical Process Control Videos
Six Sigma Green Belt Statistical Process Control Questions
Question: In the Control Phase of an LSS project, a Belt will identify key metrics that can be monitored and analyzed to give an indication that a process may be moving towards an out-of-spec condition. When he applies this approach, he is using __________________.
(A) Poisson Derivatives
(B) Inferential Statistics
(C) Kanban Analysis
(D) Statistical Process Control
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.Upgrade to a Full Membership
If you are a member, you can log in here.
Comments (11)
How to conduct SPC FOR BATCH ORDER TYPE PRODUCTION?
Try making a control chart depending on what your quality measures are.
Could you direct me to the AIAG information you mentioned in the control phase quiz? I followed the link provided but do not see the answer. I tried searching in the search bar but no results.
Larry, you don’t really need the Automotive Industry Action Group (AIAG) information. By definition out of control could be considered a certain number of points in a row on one side of the X Bar Bar or R in a control chart or a certain number of points in a row that are consistently increasing or decreasing.
I’ve seen some standards list 5 points and others list 7. The key to the question is knowing that a process shift or trend has begun if you see that behavior emerged.
I’ve updated the answer walkthrough with this.
You can find AIAG’s PDF on Academia.com here: https://www.academia.edu/7829906/AIAG_Statistical_Process_Control_SPC_2nd_Edition
Note from Admin: This question has been moved to the private member’s forum here.
How to perform SPC for Angular Dimension??
I’ve never considered it, Ranjan. Perhaps this helps?
can u explain what the difference between SPC and control charts as it is mentioned that to check causes of variation in process we use SPC that is either from natural or random causes but then why we use control charts
Think of SPC as a framework and Control charts as a tool you would use within the framework.
Control charts give you an excellent visual representation of what is going on with your process.
hello when is this article published originally
My first publication was on June 27, 2014. There have been several revisions since that time.