Process Performance Pp and Ppk tell you how your process actually did against the customer’s limits. They use all of your data, drift and shifts included. Pp looks at spread. Ppk looks at spread and centering together. If you only remember one thing, remember this: Pp and Ppk report what the customer got. Cp and Cpk report what the process could do if it stayed stable.
What Are Process Performance Pp and Ppk?
How do you know if your process can meet its specs? Process performance Pp measures the process spread vs. the specification spread. In other words, how spread out your process output is vs. what the requirements allow. Ppk adds one more question: is the process aimed at the middle?
If you’d like more depth, see these articles:
- Process Capability & Performance (Pp, Ppk, Cp, Cpk) Overview
- Process Capability (Cp, Cpk)
- Z score and process capability
Note: Use Pp & Ppk when you are initially setting up your process. They use all the data, so they still mean something before you have proven stability. After a process has reached statistical control, use Cp & Cpk. Keep reporting Pp and Ppk too. The gap between the two pairs tells you a lot (more on that below).
Let’s imagine that your process has 2 specifications: a Lower Specification Limit (LSL), which is the lowest value allowed, and an Upper Specification Limit (USL), the highest value allowed. We call the difference between the two the specification spread, sometimes referred to as the Voice of the Client. The customer sets it. Your process does not move it.
The process spread is how wide your output actually runs. For Pp and Ppk we define it as 6 standard deviations (plus or minus 3s around the mean). That covers about 99.73% of a normal process. We sometimes refer to this as the Voice of the Process.
Process Spread vs. Specification Spread
Think of the Specification Spread as the sides of your garage. They are static. They are not moving, and it is important that your process puts values inside those bounds. The Process Spread is the size of the car you are trying to fit in.
Can A Process Meet Specifications?
The answer is in the amount of variation in your process. If your process spread exceeds the specification spread, then the answer is no. However, if the process spread is less than the specification spread, then process variation is low enough for it to fit.
Process Meets Specifications: Good Potential Performance
The bell curve is narrower than the spec window. Six standard deviations fit inside LSL to USL, so Pp is greater than 1. A compact car in a two-car garage. Room on both sides.
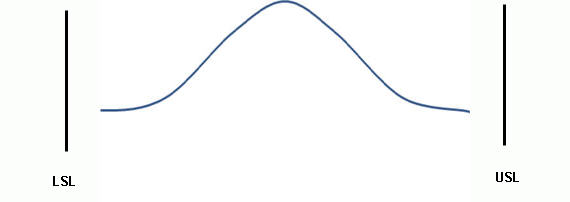
Process Does NOT Meet Specifications: Bad Potential Performance
The bell curve is wider than the spec window, so Pp is less than 1. Perfect centering will not save you. Some output will land outside the limits no matter where you aim. That is an RV and a one-car garage.
Calculating Process Performance (Pp)
Pp = (USL – LSL) / (6s)
Here s is the overall sample standard deviation of all your data, or the ‘fatness’ of the bell curve. Do not use subgroup ranges here. Pp wants every data point, pooled together, so any drift between shifts, lots, or operators shows up in s.
Notice what Pp ignores: the mean. Slide the whole curve left or right and Pp does not change. That is why you never read Pp alone.
What is a ‘Good’ Process Performance (Pp) Number?
Six Sigma quality means 6 sigmas (standard deviations) between the mean and each spec limit. That’s 12 sigmas between the LSL and the USL.
Plug that into the formula. Replace (USL – LSL) with 12s:
Pp = 12s / 6s = 2.0
So a centered Six Sigma process has a Pp of 2.0. Where does the famous 3.4 DPMO come from, then? Six Sigma assumes the mean drifts about 1.5 sigma over the long run. That leaves 4.5 sigma to the nearest limit, which is a Ppk of 1.5. A 4.5 sigma tail is 3.4 defects per million. So you will see both numbers: 2.0 for Pp and 1.5 for long-term Ppk. They describe the same process.
In practice, most customers set the bar lower. 1.33 is a common minimum. Many automotive customers want 1.67 or higher on a new process.
Is the Process Acceptable? Ppk (Performance)
Ppk measures how close the process mean sits to the nearest specification limit. In other words, does this process deliver acceptable results where it is actually aimed?
A narrow process that is parked against one limit still makes defects. Ppk catches that. Pp does not.
Calculating Ppk
Ppk = min[ (USL – x̄) / 3s , (x̄ – LSL) / 3s ]
Calculate both sides. Report the smaller one. The worse side is the side that makes your defects.
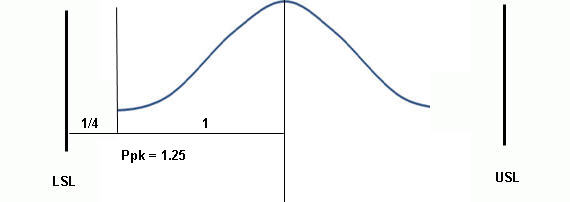
Process Mean close to USL
If your Process Mean (central tendency) is closer to the USL, the upper side wins: Ppk = (USL – x̄) / 3s, where x̄ is the Process Mean.
Process Mean close to LSL
If your Process Mean (central tendency) is closer to the LSL, the lower side wins: Ppk = (x̄ – LSL) / 3s, where x̄ is the Process Mean.
One-sided spec? Only a USL (like impurity) or only an LSL (like pull strength)? Then there is no Pp. Ppk is just the one side you have.
Interpreting Ppk Scores
A Ppk of 1 means there is exactly “half of a bell curve” (3 standard deviations) between the process mean and the nearest specification limit. It does not tell you the process is centered. For that, compare Ppk to Pp:
- Ppk = Pp: the process is centered.
- Ppk less than Pp: the process is off center. The bigger the gap, the further off.
- Ppk greater than Pp: impossible. Check your math.
- Ppk below zero: the mean is outside the spec limits. Most of your output is scrap.
Here is how Ppk lines up with sigma distance and defect rate. The defect rates assume normal data and count only the nearest tail. If the process is centered, double them to get both tails.
| Ppk | Sigmas to nearest limit (Z) | Defects per million, nearest tail | What it means |
|---|---|---|---|
| 0.33 | 1.0 | 158,655 | Badly off target or too wide. Fix it now. |
| 1.00 | 3.0 | 1,350 | Barely fits. Any shift makes defects. |
| 1.33 | 4.0 | 32 | Common minimum for acceptance. |
| 1.50 | 4.5 | 3.4 | Six Sigma long-term (after a 1.5 sigma shift). |
| 1.67 | 5.0 | 0.29 | Strong. Typical target for a new process. |
| 2.00 | 6.0 | 0.001 | Six Sigma short-term, centered. |
Preparing for a Six Sigma exam? Get the one-page Cp, Cpk, Pp, Ppk cheat sheet.
Formulas, how to judge the number, the exam rules, and a worked example on one printable page. Enter your email and I'll send it now.
You'll also get my weekly Six Sigma newsletter. Unsubscribe anytime.
Pp vs. Cp: Long-Term vs. Short-Term Sigma
Pp and Cp use the same formula. Ppk and Cpk use the same formula. The only difference is which standard deviation you plug in.
- Pp, Ppk: overall (long-term) s. The standard deviation of every data point, pooled together.
- Cp, Cpk: within-subgroup (short-term) sigma. Usually estimated from a control chart as R-bar / d2 or s-bar / c4. It only sees the variation inside each subgroup.
Overall s includes everything the within-subgroup sigma misses: shift changes, tool wear, new material lots, Monday mornings. So overall s is almost always the larger of the two. That means Ppk is almost always less than or equal to Cpk.
Read the gap. If Cpk is 1.4 and Ppk is 1.3, the process is behaving. If Cpk is 1.4 and Ppk is 0.7, something is moving the mean between subgroups. The process is not stable, and the Cpk is a promise you are not keeping. Go look at the control chart before you report either number.
Worked Example: Process Performance Pp and Ppk on a Bolt Line
A plant makes bolts with a target length of 50.00 mm. The spec is 49.80 to 50.20 mm. In the Measure phase, the team pulls 1,500 parts across several weeks.
Baseline: mean = 50.10 mm, overall s = 0.10 mm.
- Pp = (50.20 – 49.80) / (6 x 0.10) = 0.40 / 0.60 = 0.67
- Upper side = (50.20 – 50.10) / (3 x 0.10) = 0.10 / 0.30 = 0.33
- Lower side = (50.10 – 49.80) / (3 x 0.10) = 0.30 / 0.30 = 1.00
- Ppk = the smaller side = 0.33
Pp of 0.67 says the process runs 0.60 mm wide in a 0.40 mm window. Too wide. Ppk of 0.33 says it is also aimed high. The upper limit is only 1 sigma from the mean, so roughly 16% of the bolts come out long. Another 0.1% come out short. That is a sorting operation, not a process.
The team also runs an X-bar and R chart. Within-subgroup sigma comes out at 0.06 mm. That gives Cp = 0.40 / 0.36 = 1.11 and Cpk = 0.10 / 0.18 = 0.56. The gap between Cp (1.11) and Pp (0.67) points at something moving between subgroups. The team finds tool wear between tool changes.
After improvement: a tool change schedule and a new offset procedure. Mean = 50.00 mm, overall s = 0.05 mm.
- Pp = 0.40 / (6 x 0.05) = 0.40 / 0.30 = 1.33
- Ppk = 0.20 / (3 x 0.05) = 0.20 / 0.15 = 1.33
Pp doubled. Ppk went up four times. Pp now equals Ppk, so the process is centered. Each limit is 4 sigma away, which is about 63 defects per million across both tails. In Control, the team keeps tracking Ppk monthly to prove the gain holds.
Pp, Ppk In Relation to Z Scores
Ppk can be determined by dividing the Z score to the nearest spec limit by three. A z score is the same as a standard score: the number of standard deviations a value sits from the mean.
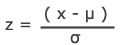
Z = (x – mean of the population) / standard deviation.
Ppk = (USL – µ) / 3σ = ZUSL / 3, when the USL is the nearer limit.
Flip it and Z = 3 x Ppk. A Ppk of 1.33 puts the nearest limit 4 sigma out. Look up Z = 4 in a Z table and you get about 32 defects per million in that tail. A Ppk of 1.0 is Z = 3, or about 1,350 per million in that tail.
Common Mistakes with Pp and Ppk
- Reading Pp without Ppk. Pp ignores the mean. A great Pp on a process parked against a limit still ships defects.
- Using the wrong sigma. Pp and Ppk use the overall s of all the data. If you plug in R-bar / d2, you calculated Cp and Cpk.
- Too little data. Thirty parts from one morning is not long-term. Collect across the sources of variation you expect: shifts, lots, operators, tool changes.
- Ignoring the shape. The Z table only works for roughly normal data. Check a histogram or normal probability plot first. Skewed data needs a transformation or a non-normal method.
- Treating an unstable Ppk as a forecast. Ppk tells you what happened. If the process is out of control, it does not tell you what happens next month.
- Comparing across products without the spec. A loose tolerance can give a high Ppk to a sloppy process. Compare indices only when you know the specs behind them.
Exam Tips for Process Performance Pp and Ppk
- Pp = (USL – LSL) / 6s. Ppk = the smaller of (USL – x̄) / 3s and (x̄ – LSL) / 3s.
- “Overall,” “long-term,” or “total” standard deviation points to Pp and Ppk. “Within,” “short-term,” or “R-bar / d2” points to Cp and Cpk.
- Ppk is never larger than Pp. They are equal only when the process is centered.
- Z to the nearest limit = 3 x Ppk.
- Specification limits come from the customer. Improving the process changes the indices, never the specs.
- Watch for a mean outside the limits. The answer may be a negative Ppk.
ASQ Six Sigma Green Belt Process Performance Questions
Question: Which of the following measures is increased when process performance is improved?
(A) Variability range
(B) Capability index
(C) Repeatability index
(D) Specification limits
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.Upgrade to a Full Membership
If you are a member, you can log in here.
Is this on your exam? Try 3 practice questions.
Real questions from the Six Sigma Study Guide question bank, with the full explanation.
Question 1. Which of the following measures is increased when process performance is improved?
Question 2. Once the team has conducted their initial data collection they will have more details around process performance, potential causes and potential goals. Where is this data incorporated in order to describe the issue accurately?
Question 3. You are producing a line of snack foods that requires an adhesive label. The adhesive strength must be strong enough to stay on the package but not so strong that it jams the machine, which puts it between 0.25 lbs and 4.5 lbs. You pull a sample of 100 labels and find a variance of 0.66 lbs squared. What is the process performance?
Want the full question bank, organized by exam topic, with an explanation for every answer? See the Green Belt study guide or the Black Belt study guide.
Comments (40)
Very helpful ..
Glad to be of service, Amrita!
Very helpful……..thank you so much.
Glad it helped!
Very helpful, Nice
If a process has a variance of 4 units and a specification
of 96 ± 4, what is the process performance index (Pp)?
(A) 0.33
(B) 0.66
(C) 1.00
(D) 1.50
Idris- can you tell me the steps you took to try to solve this?
USL = 96+4 = 100
lSL = 96-4 = 92
VARIANCE = 4
Pp = (USL – LSL)/(6 x sq. root of VARIANCE)
= (100 – 92)/(6 x 2)
= 0.666
thankyou so much for providing solutions.
I’ve added this question and a full answer walkthrough to the thousands of others available in the paid membership areas.
0.66
USL = 100
LSL = 92
Variance is 4
Standard deviation = Square root (4) = 2
Pp = (USL-LSL)/ (6*Standard deviation)
Pp= (100-92) / ( 6*2)
Pp= 8/ 12
Pp = 0.6667
Pp is 0.66
0.66
Hi Ted Hessing.
If we calculate like this, the Ppk and Cpk is equal?
Because the recipe to calculate them are the same.
Hi Pham, Can you show me an example below?
It is the same calculation:
Calculating CPK (from https://sixsigmastudyguide.com/process-capability-cp-cpk/):
Cpl = (Process Mean – LSL)/(3*Standard Deviation)
Cpu = (USL – Process Mean)/(3*Standard Deviation)
Calculating PPK (from https://sixsigmastudyguide.com/process-performance-pp-ppk/):
Process Mean close to USL
If your Process Mean (central tendency) is closer to the USL, use: Ppk = [ USL – x(bar) ] / 3 s, where x(bar) is the Process Mean.
Process Mean close to LSL
If your Process Mean (central tendency) is closer to the LSL, use: Ppk = [x(bar) – LSL ] / 3 s, where x(bar) is the Process Mean.
What would the Ppk be for a process with average of 50, standard deviation of 5, and specification limits of 36 and 72 ?
To calculate Ppk, we use the formula:
Ppk = min[(USL - μ) / (3σ), (μ - LSL) / (3σ)]Given:
Calculations:
Ppk = min(1.467, 0.933) = 0.933
So, the Ppk for this process is approximately 0.933. This value suggests that the process is not fully capable of consistently meeting specifications, especially near the lower specification limit.
0.93
PpK is 23.3333
Great guide, thanks for your help!
You’re welcome, Xuade!
What is the best value and acceptable range of Cp ,Cpk & Pp,PPK
Here’s a refined summary of the best target values and acceptable ranges for Cp, Cpk, Pp, and Ppk based on industry standards and Six Sigma practices:
Cp (Process Capability – Potential):
Use: Short-term potential (spread only)
Acceptable Range: ≥ 1.33 (some industries use ≥ 1.50 for new processes)
Desired Target: ≥ 2.00 (Six Sigma level)
Cpk (Process Capability – Actual):
Use: Short-term capability (spread + centering)
Acceptable Range: ≥ 1.33 for mature processes; ≥ 1.67 for new/critical ones
Desired Target: ≥ 2.00 (Six Sigma)
Pp (Process Performance – Potential):
Use: Long-term performance (spread only)
Acceptable Range: ≥ 1.33
Desired Target: ≥ 1.50 to 2.00
Ppk (Process Performance – Actual):
Use: Long-term performance (spread + centering)
Acceptable Range: ≥ 1.33 for stable processes; ≥ 1.67 for critical/high-reliability ones
Desired Target: ≥ 2.00 (Six Sigma)
In summary:
1.00 to 1.33: Barely capable; may require more inspection or control.
≥ 1.33: Generally acceptable for established processes.
≥ 1.67: Preferred for new, critical, or safety-sensitive applications.
≥ 2.00: Represents world-class, Six Sigma-level performance.
Remember, Cp and Cpk use short-term variation and assume the process is in control, while Pp and Ppk reflect long-term performance and include all variation. That’s why Cp/Cpk typically appear more favorable than Pp/Ppk.
what if the CPK value is at 5.63 and Ppk at 2.58 but the xbar chart is having some points out of control limits.
How I should evaluate?
This is a fascinating and important scenario that highlights the distinction between process capability/performance indices and process stability.
Understanding the Metrics
How to Evaluate
The key issue here is process stability. Even though Cpk and Ppk are high, if your X̄ chart shows points outside control limits or non-random patterns, your process is statistically not in control.
Here’s how to evaluate and address the situation:
Conclusion
High capability numbers are only meaningful when the process is stable. Prioritize investigating and correcting the sources of instability shown in your X̄ chart. Once the process is stable, your Cpk and Ppk values will more accurately reflect true performance.
Additionally, if you’re interested in preparing for your certification, consider our comprehensive courses:
Being a more difference between Cpk and Ppk looks like special cause exists in the process. Remove those special cause/s and again check whether any point going out of UCL/LCL.
If then there is marginal difference between Cpk and Ppk and any point still showing out of control limit then it it should be acceptable since absolute values of Cpk and Ppk are much higher than six sigma level.
The post has the right idea, but needs a bit of clarification.
What’s Right
What Needs Fixing
So, first get your process stable by removing special causes. Then check Cpk and Ppk. Only when the process is in control do those values really tell you how capable your process is.
For more details, check out: Process Capability & Performance and X Bar R Control Charts.
Great example about a car and garage, it is much simpler to understand!
I’m glad it helps, Kate!
Hello, I like your articles. But it seems like you had a typo hidden:
This is what happens when your specification spread does not match your specification spread!
I think you wanted to say:
This is what happens when your process spread does not match your specification spread!
BR,
Ivan
Thank you, Ivan for the feedback, we have updated the sentence.
Thanks
When do we get Ppk form OSAT?
What is the minimum Sample Size to compute the Ppk?
Pablito, tell me more of what you are thinking here. I don’t want to give people direct answers to their homework problems. I do want to help people think through these concepts.
Cp is generally referred to as Process Capability. Pp as Process Performance. In this article, Pp is however called Process Capability. Is that a typo?
Great observation, and thank you for pointing that out!
You’re absolutely right: Cp is commonly known as Process Capability, which measures how well a process can potentially perform if it were centered and in statistical control. Pp, on the other hand, stands for Process Performance, and it reflects the actual performance of the process over a period of time, regardless of whether the process is in control.
If the article refers to Pp as Process Capability, that may indeed be a typo or a misstatement. The two indices are related but distinct in their application and interpretation. We always strive for clarity in our educational content, so I appreciate your attention to detail.
If you have any more questions or spot anything else, feel free to reach out!
Is there a guide available that shows how to calculate cpk for runout on a sample?
Hi Gloria Peralta,
Runouts are specified with a single value: a not-to-exceed value. For example, the specification for runout could be 0.0005 inches. This means that the Upper Spec Limit (or USL) = 0.0005 in and the Lower Spec Limit is obviously zero.
Assuming that we have a normal distribution, then Cpk for runout:
Cpk = Cpu = (USL – Mean)/(3 * Sigma),
where, Sigma is the rational subgroup estimate of sigma (often referred to as the short-term standard deviation).
Thanks
How did fix limitations of Cpk => 1.33..?
Is there any calculations / rules for this..?
I’m not sure I understand what you’re asking here. Can you elaborate?