How to determine baseline project sigma is one of the key aspects of the Measure phase. Baseline sigma calculation is part of the Data collection plan.

Sigma, denoted by the symbol σ (a Greek alphabet), represents the standard deviation of a population. Primarily, it characterizes the dispersion of a set of data values with respect to the mean. It refers to the mathematical concept of standard deviation.

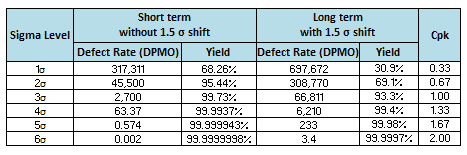
Six Sigma is derived from the normal or bell curve in statistics, where each interval shows one sigma or one standard deviation. Moreover, Sigma is a statistical term that refers to the standard deviation of a process about its mean. In a normally distributed process, 99.73% of measurement will fall within ±3σ, and 99.99932% will fall within ±4.5σ.

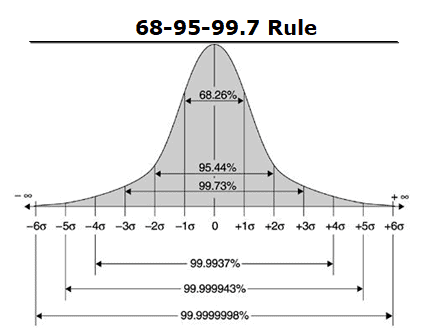
The 68-95-99.7 rule, also known as an empirical rule used to remember the percentage of values that lie within a band around the mean in a normal distribution with a width of one, two, and three standard deviations, respectively.

Why Would You Want Your Baseline Sigma to be 1, 2, or 3?

You would want your baseline sigma to be 1, 2, or 3 because those often reveal a bad process, and you would like your team to be able to see an improvement in the process at the end of the project.

What is the Reason behind Calculating the Sigma Value?

The value in making a sigma calculation is that it abstracts your level of quality enough so that you can compare levels of quality across different fields (and different distributions.) In other words, the sigma value (or even DPMO) is a universal metric, that can help you with the industry benchmark/competitors.

Does the Data Type (Discrete/Continuous Data) Have Any Effect on Calculating the Sigma Value?

Data type does NOT have an effect on the sigma value so long as we are counting the total number of opportunities and defects properly.

How to Determine the Baseline Project Sigma for Discrete Data

You can determine the process capability through the number of defects per opportunity. The acceptable number to achieve Six Sigma is 3.4 Defects Per Million Opportunities (DPMO).

• Unit – the item produced or created.
• Defect – anything that causes a failure (i.e. misses the requirements of the customer.)
• Opportunity – the number of critical quality measures we are counting on each opportunity in defects. If there are 4 types of defects, this value is 4.
• DPO = Defects/(Units * Opportunity)
• DPMO = (Defects / Units * Opportunities) * Total 1,000,000
• Yield = 1-DPO (It is the ability of the process to produce defect-free units).

Determine if Zero defects are needed or if there is partial credit.

• If the process is only considered correct if there are no defects at all (100% correct), then use the DPMU calculation (defects per million units). DPMU = (Defects / Units) * 1,000,000
• If partial credit is received for meeting some of the requirements: use the DPMO calculation (defects per million opportunities). DPMO = (Defects / Units * Opportunities) * Total 1,000,000

Examples of Baseline Sigma for Discrete Data

Example: XYZ is a commercial flight carrier operating 10,000 flights a day. There are three defect opportunities like late arrival, lost luggage, and poor in-flight experience. Let’s assume 10,000 defects have been identified. Calculate process sigma level.

• Unit or sample size = 10,000 flights a day
• Defects types = 3 (could be a late arrival, lost luggage, poor in-flight experience).
• Opportunities = 10,000 flights * 3 kinds of defect opportunities = 30,000
• Defects: 10,000 defects
• DPMO = (Defects / Units * Opportunities) * 1,000,000
• DPMO= (10000 /10000*3) * 1,000,000 = (1/3) * 1M. = 333,333 defects per million opportunities.
• From the below chart, 333,333 DPMO translates to a sigma between 1.95 and 1.9.

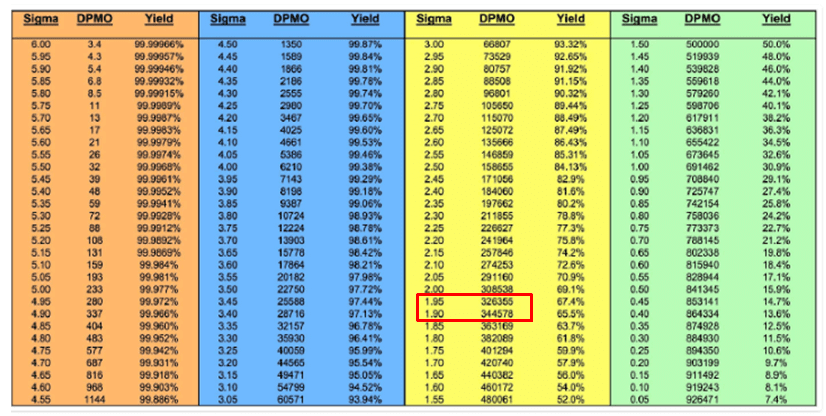
• Or in excel use the formula = NORMSINV (1- (defects/ sample size * Number of defect opportunities per unit in the sample) + 1.5

Excel Template Download to Determine Baseline Sigma for Discrete Data

Question: A company is currently operating at a 2 sigma level of quality. What will be the number of defects expected if they are able to improve to a 3 sigma, 4 sigma and 5 sigma level of quality?

Answer: A sigma of 2 equates to 308,538 defects per million opportunities or 69.2% yield. Further, A Sigma of 3 = 66,807, a sigma of 4 = 6,210, and a sigma of 5 = 233. (refer above table).

How to Determine Baseline Project Sigma for Continuous Data

Process Capability determines if a process meets the needs of the customer. Process capability compares the output of an in-control process to the specification limits. We can say the process is capable when almost all the measurements fall within the specification limits. Cp and Cpk are considered short-term potential capability measures for a process.

In Six Sigma, we want to describe the quality of a process in terms of sigma because this gives us an easy way to talk about how capable a process is at using a common mathematical framework.

Cpk is a measure to show how many standard deviations the specification limits are from the center of the process. 

• C_plower = (Process Mean – LSL)/(3*Standard Deviation)
• C_pupper = (USL – Process Mean)/(3*Standard Deviation)
• Cpk is the smallest value of the Cpl or Cpu:  C_pk= Min (C_pl, C_pu)

The main purpose of C_pk is to determine how well a process performs when compared to its specification limits and the natural variability of the process. A larger Cpk is always better–it infers a lower probability of any item being outside the specification limits.

Process sigma = 3* C_pk. Hence, we generally want a  C_pk of at least 1.33 [4 sigmas] or higher to satisfy most customers.

Examples of Baseline Sigma for Continuous Data

Example: The specification limit of rubber sheets is 5±1cm. The operator randomly recorded 4 subgroups of values every half an hour in three shifts. While the average mean is 4.7, and the short-term pooled standard deviation is 0.2 cm. Calculate the process sigma level.

• USL=6cm
• LSL = 4cm
• Standard deviation σ_R= 0.2 cm
• Process mean = 4.7cm
• C_plower = (Process Mean – LSL)/(3*Standard Deviation) = 1.16
  C_pupper = (USL – Process Mean)/(3*Standard Deviation) = 2.16
• Cpk = min (Cpu, Cpl) = 1.16
• Sigma = 3 * 1.16 = 3.5

Excel Template Download to Determine Baseline Sigma for Continuous Data

Why Use Sigma Instead of Percent?

Why can’t we just use the percentage reduction in the defects to assess the process rather than the sigma value?

The answer is that, of course, you can. Many people do. But it has to make sense for your business.

However, measuring the change in terms of sigma allows you to judge improvements and opportunities in a more consistent manner.

Important Videos for How to Determine Baseline Project Sigma