Regression Analysis

A Regression Analysis is a way of gauging the relationships between different variables by looking at the behavior of the system. There are many analysis techniques used to determine the relationship between dependent and independent variables. However, a Regression Analysis is one of the best. For example, transformations can be used to reduce the higher-order terms in the model.

Remember the equation for a line that you learned in high school? Y = mx + b where m is the slope of the line, and b is the point on the y-axis where the line intercepts. Given the slope (m) and the y-intercept (b), you can plug in any value for X and get a result y. Very simple and very useful. That’s what we are trying to do in root cause analysis when we say “solve for y.”

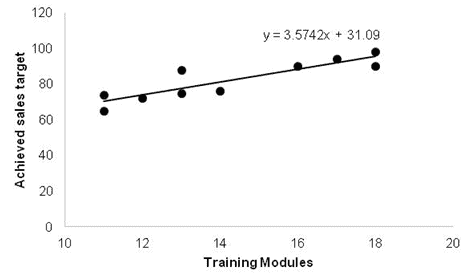
Though statistical linear models are described as a classic straight line, often linear models are shown as curvilinear graphs. While non-linear regression aka Attributes Data Analysis is used to explain the nonlinear relationship between a response variable and one or more than one predictor variable (mostly curve line).

Unfortunately, real life systems do not always boil down to a simple math problem. Sometimes you just have a collection of points on a graph, and your boss tells you to make sense of them. That’s where regression analysis comes into play; you are basically trying to derive an equation from the graph of your data.

“In the business world, the rear view mirror is always clearer than the windshield.”

Warren Buffet

Linear Regression Analysis

The easiest kind of regression is linear regression. Imagine that all of your data is lined up in a neat row. If you could draw a straight line through all points that would model a simple equation Y = mx + b that we talked about earlier. That would give you a model that would predict what your system would do given any input of x.

But what if your data doesn’t look like a line?

In that case, Multiple linear regression is an extension of the methodology of simple linear regression.

Method of Least Squares

The Method of least squares is a method to create the best possible approximation of a line given the data set.

How well the created line fits the data can be determined by the Standard Error of Estimate. The larger the Standard Error of the Estimate, the greater the distance of the charted points from the line.

The normal rules of Standard Deviation apply here; 68% of the points should be within +/- 1 Standard Error of the line; 95.5% of the points within +/- 2 Standard Error.

For more examples of Least Squares, see Linear Regression.

Coefficient of Determination (R^2 aka R Squared)

The Coefficient of Determination provides the percentage of variation in Y that is explained by the regression line.

Coefficient of Correlation is r.

Just take the square root of the Coefficient of Determination – Sqrt(R Squared)

Go here for more on the Correlation Coefficient.

Measuring the validity of the model

Use the F statistic to find a p-value of the system. The degrees of freedom for the regression are equal to the number of Xs in the equation (in a linear regression analysis, this is 1 because there is only 1 x in y=mx+b).

Null Hypothesis: Suggests that there is no statistical significance between the two variables in the study.

Alternative Hypothesis: Suggests that there is statistical significance between the two variables in the study.

The smaller the p-value, the better. But really, you judge this by finding the acceptable level of alpha risk and seeing if that % is greater than the p-value. A P-value of 0.05 means that 5% of the time, we will falsely reject the null hypothesis. It means 5% of the time we might falsely have concluded a relationship.

For example, if your alpha risk level is 5% and the p-value is 0.014, then we can reject the null hypothesis and may conclude that there exists a relationship between the variables. – in this case, you’d accept the line as there is a significant relationship between the variables.

Additional Helpful Resources

Residual Analysis: “Since a linear regression model is not always appropriate for the data, assess the appropriateness of the model by defining residuals and examining residual plots.”

What is the difference between Residual Analysis and Regression Analysis?

Regression models, a residual measures how far away a point is from the regression line. In a residual analysis, residuals are used to assess the validity of a statistical or ML model. The model is considered a good fit if the residuals are randomly distributed.

https://www.scaler.com/topics/data-science/residual-analysis/

• When should we use regression analysis?
• Regression output interpretation in Minitab
• Extrapolation beyond a regression model

Regression Analysis and Correlation Videos

ASQ Six Sigma Black Belt Exam Regression Analysis Questions

Question: In regression analysis, which of the following techniques can be used to reduce the higher-order terms in the model?

A) Large samples.

B) Dummy variables.

C) Transformations.

D) Blocking.

Answer:

Transformations. Once you have identified a working equation for the system, you can often reduce the higher-order terms (the messier and more difficult work) into equations that are easier to work by transforming them.