Non-Linear Regression, aka Attributes Data Analysis

What is Non-Linear Regression?

Non-linear regression, aka Attributes Data Analysis, is organized into discrete data types (groups or categories).

When do you use Non-Linear Regression, aka Attributes Data Analysis?

Simple Linear regression is a statistical technique used to estimate the mathematical relationship between a dependent variable (usually denoted as Y) and an independent variable (usually denoted as X) and is denoted with a straight line y=mx+b. Although statistical linear models could describe the classic straight line, most statistically linear models are not represented by straight lines but by curvilinear graphs. Non-linear regression, aka Attributes Data Analysis, is used to explain the nonlinear relationship between a response variable and one or more predictor variables (mostly curve line). In other words, a regression model is called “non-linear” if the derivative of the model depends on one or more parameters.

Specifically, use non-linear regression instead of ordinary least square regression when one cannot adequately model the relationship with linear parameters.

DO NOT USE Linear Regression for attribute data analysis- because this assumes the response variable is continuous.

For instance, Analyze attribute data using logit, probit, logistic regression, etc., to investigate sources of variation.

Logistic Regression

Logistic regression is a method used to predict a dependent variable for a given set of independent variables, such that the dependent variable is categorical. This method is widely used in machine learning algorithms.

Logistic regression is similar to linear regression; however, logistic regression predicts categorical data (like true or false), whereas linear regression predicts continuous data. Hence, the dependent variable in logistic regression is categorical, but in linear regression, the dependent variable is always continuous. Logistic regression uses a logit transformation on the dependent variable to fit a linear regression model.

The outcome of logistic regression is always categorical when the resultant outcome always has only two possible values of 0 or 1.  In logistic regression, the graph is not a linear line, but the line looks like a curve goes between 0 and 1. The curve is called the “S” curve and is also called as Sigmoid curve.

Although logistic regression tells the probability, it is most commonly used for classification. The team has to determine the threshold value if the probability of the event happening between 0 and 1, then based on the threshold value event is to be classified as 0 or 1.

For example, if the threshold value is 0.5, then any value between 0.5 and 1 it should be classified as 1, similarly any value below 0.5 then it should classify as 0

Logistic Regression calculation

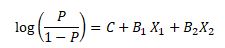
P ranges between 0 and 1; it represents the probability of an event to happen.

X₁ and X2 are the independent variables that determine the occurrence of an event.

C is the constant

B₁, B₂ represents the respective coefficients of X₁, X₂

Additional Notes on Logistic Regression

• The regression coefficients for logistic regression models are based on MAXIMUM LIKELIHOOD ESTIMATION.
• Sample sizes should be at least 50 per variable.
• Logistic Regression is best for:
  • Binary with two categories
  • Ordinal or Nominal w/ 3 or more categories

Logistic Regression Example

We can use Non-linear regression models in the analysis phase of DMAIC. For example, the American Cancer Institute wants to predict the chances of throat cancer based on the smoker’s average cigarette consumption per day. From the below random data, 0 indicates no cancer, and 1 indicates throat cancer.

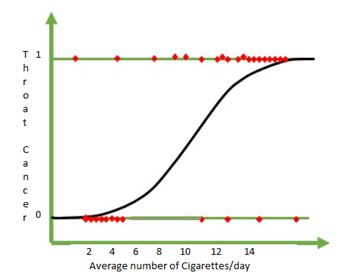
From the above data, logistic regression helps to assess what level of cigarette consumption leads to throat cancer. Moreover, from the above graph, one can say if the number of cigarette consumption is more than eight, it leads to throat cancer, and if cigarette consumption is below eight, there is no cancer. Hence, logistic regression is the best method for complex problems.

Certainly, we have to use statistical tools (like R and Minitab) to model the logistic regression.

Using the formula

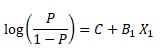
Suppose we get the following values (random values) from the above information

C= -0.100245

B1= 0.1814

If we want to predict 2.6

=-0.100245+ 0.1814*2.6= -0.53081

Use the sigmoid function to find the probability

Since the f(z ) value is 0.37 (towards zero), we can predict 2.6, there will be no chance of throat cancer.

Logit Analysis

Logit regression is a model where the dependent variable is qualitative, In other words, dependent variable is categorical. If the dependent variable is categorical in two parts it is binary logistic regression, for more than two categories it is a multinomial logit regression.

Formula for P=f(z)

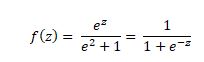
f is the cumulative distribution function for a standard logistic random variable.

z= β₀+ β₁x₁+ β₂x₂+………………+ β_nx_n

β₀ is the intercept and β_{1 ,}β_2,β₃ are the slopes against independent variable

f is a function : 0<f(z)<1, for all z

Logit analysis Example

A cardiology doctor wants to predict the chances of life threat with cholesterol. He collected data after specific periods having different cholesterol levels for both alive and dead patients. The response is a binary variable (i.e. alive or dead)

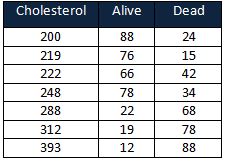
Find the logarithm base 10 for cholesterol

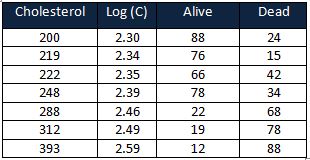
Calculate the proportion of dead patients= dead/(alive+dead)

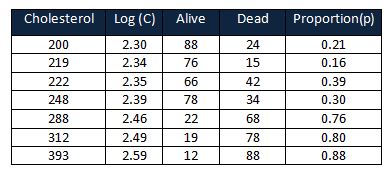
Calculate the logit (p) = log(p/1-p)

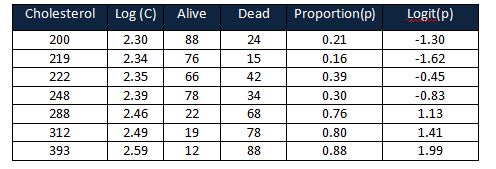
Calculate the slope and intercept using logit values and log values of cholesterol.

We must use statistical tools (like R and Minitab) to model the logistic regression.

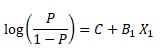
Once the model is ready, Use the sigmoid function to find whether the chances of the patient is dead or alive for a particular cholesterol level.

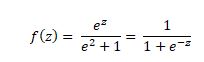
Probit Analysis

The probit model was first introduced by Chester Bliss in 1934, but Ronald Fisher proposed the maximum likelihood method as an appendix to Bliss in 1935.

A probit model is a popular ordinal or binary response model specification. This model, which employs a probit link function, was estimated using the maximum likelihood method, hence this estimation was named probit regression.

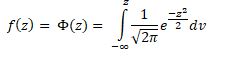
z= β₀+ β₁x₁+ β₂x₂+………………+ β_nx_n

Where f is the standard normal cumulative distribution function (cdf)

Probit Analysis Example

A coaching center interested in students’ GMAT (Graduate Management Admission Test ) scores and admission into the business school. The response is a binary variable (i.e, admit or no admission into the business school)

Firstly, find the logarithm base 10 for the GMAT Score

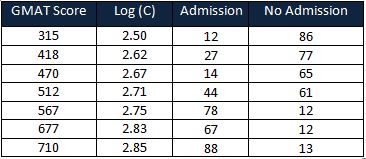
Then, calculate the proportion of no admission = No admission /(admission + no admission)

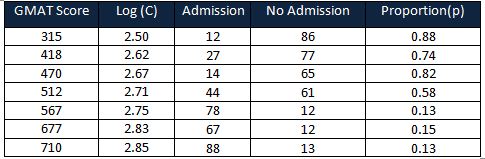
Lastly, calculate the Probit values using the chart

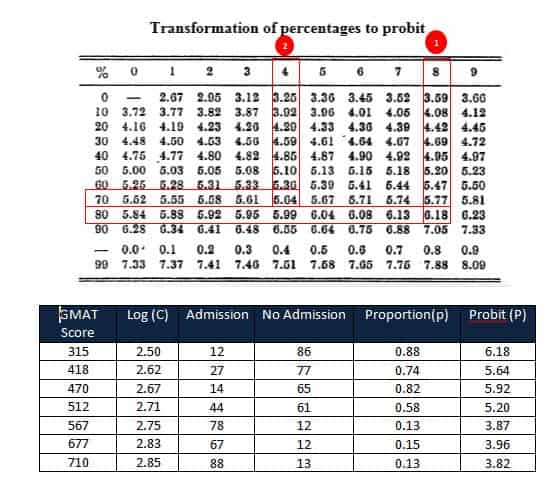
Calculate the slope and intercept using probit values and log values of the GMAT score.

We must use statistical tools (like R and Minitab) to model the logistic regression.

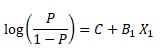
Once the model was established, the probit function was to find whether the chances of student admission or no admission into the business school for a particular GMAT score.

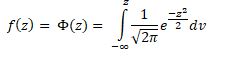
Difference between logit and probit

Both logit and probit models yield almost the same results. The logit and probit functions are increasing, and both functions increase relatively quickly in the central portion and relatively slow at the extremities, and both functions lie between 0 and 1. While the only key difference between the logit and probit models is in the use of the link function

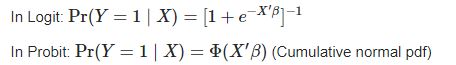
In other words, the logit model will have slightly flatter tails compared to the probit model. 

When you’re ready, there are a few ways I can help:

First, join 30,000+ other Six Sigma professionals by subscribing to my email newsletter. A short read every Monday to start your work week off correctly. Always free.

—

If you’re looking to pass your Six Sigma Green Belt or Black Belt exams, I’d recommend starting with my affordable study guide:

1)→ 🟢Pass Your Six Sigma Green Belt​​

2)→ ⚫Pass Your Six Sigma Black Belt ​​​

You’ve spent so much effort learning Lean Six Sigma. Why leave passing your certification exam up to chance? This comprehensive study guide offers 1,000+ exam-like questions for Green Belts (2,000+ for Black Belts) with full answer walkthroughs, access to instructors, detailed study material, and more.

​ Join 10,000+ students here.