A Paired T-Distribution and Paired T-Test (Paired T-Distribution, Paired T-Test, Paired Comparison Test, Paired Sample Test) are statistical methods that compare the mean and standard deviation of two matched groups to determine if there is a significant difference between the two groups. In other words, they test whether or not the average difference between the two measurements is statistically significant from zero.
Student’s T-Distribution is used to find confidence intervals for the population mean when the sample size is less than 30 and the population standard deviation is unknown. Further, the Student’s T-Test is divided into paired and unpaired T-Tests.
Also, See Student’s T-Test–for when samples are <30 in size.
When the sample groups are not independent, the appropriate method to test for differences between the groups is known as a paired comparison test (or paired T-test or paired sample test).
Furthermore, use the Paired T-Distribution and Paired T-Test to identify if a change has significantly impacted a process. The Paired T-test is similar to a 1-sample T-test. A 1-sample T-Test compares one sample mean. At the same time, a paired T-Test calculates the difference between paired values and then performs a 1-sample T-Test on the differences.
When to use Paired T-tests and Paired T-distributions
The Paired T-distributions, Paired T-tests, Paired Comparison Tests, and Paired Sample Tests are parametric procedures. Paired Samples T-tests are used when the same group is tested twice. It is often used in “before and after” designs where the same individuals are measured before and after a treatment or improvement to see if changes occurred over time.
Paired T-Distribution and Paired T-Test Assumptions
- Two repeated or matched samples, in other words, must have a before and after design or matched pairs.
- Paired samples T-tests can have only two groups. Use ANOVA for more than two measures.
- The non-negotiable assumption for the paired samples is dependent variable must be quantitative.
- The paired T-Test assumes no extreme outliers.
- The dependent variable’s sampling distribution should be normally distributed. If the data is non-normal, use the Wilcoxon test.
- A dependent variable is a continuous variable measured at an interval or ratio.
- Unlike the independent samples T-Test, there is no assumption for homogeneity of variance with a paired sample T-Test.
What is the Hypothesis of the Paired T-test?
- The Null Hypothesis for a paired T-test is that the average difference between the two population means is zero (0). In other words, there is no significant difference between the two population means.
- The Alternative Hypothesis for a paired T-Test–there is a significant difference between the two population means.
How to conduct a Paired T-test
- Establish the Null Hypothesis and Alternative Hypothesis
- Determine the significance level
- Calculate the difference between each observation in the two groups
- Then, compute the mean difference (x̅ – µ)
- Calculate the standard deviation of differences (s) and then calculate the standard error, i.e., s/√n (where n is the sample size)
- Compute the T-Statistic, t= (x̅ – µ)/ s/√n
- Determine t critical value with n-1 degrees of freedom
- Finally, interpret the result. If the test statistic falls in the critical region, reject the null hypothesis.
Hypothesis Testing
A Tailed Hypothesis is an assumption about a population parameter. The assumption may or may not be accurate. One-tailed Hypothesis is a test of a hypothesis where the area of rejection is only in one direction. Two-tailed tests measure against the alternative that there is a significant difference between the two population means. The selection of one or Two-tailed tests depends upon the problem.
Example of Two-tailed Paired T-test
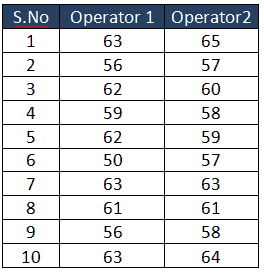
Example: Two operators check the same dimension on the same sample of 10 parts. Below are the results. Is there a significant operator measurement error? Test at the 5% significance level.
Solution Details:
We need to calculate the T-Statistic value using t= (x̅ – µ)/ s/√n and then compare it to a table value t critical.
- H0 =There is no significant measurement error between the two operators.
- H1 =There is a significant measurement error between the two operators.
- n=10
- DF (degrees of freedom) = n-1 ; 10-1 =9
- Significance level =5%
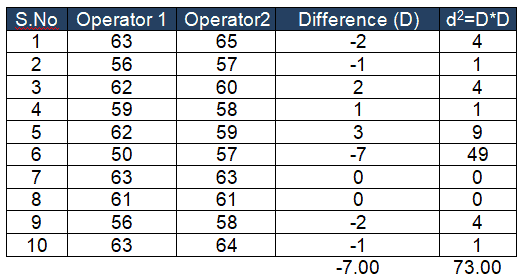
Calculate the difference between each observation in the two groups
Compute the mean difference (x̅ – µ)
- µ (mean of first test) = 59.5 ; take the average of the 10 data points in Op1
- x̅ (mean of new test) = 60.2 ; take the average of the 10 data points in Op2
- x̅-µ = 60.2 – 59.5 =0.7
Calculate the Standard Deviation of differences (s)
- D= -7 ; d2=73
- Use sd = sqrt [ (Σ(di – d)2 / (n – 1) ] where di is the difference for pair i, d is the sample mean of the differences, or s=( √ ((n*d2)-D2)/df) / √(n)
- s = (√ ((10*73) -(-7*-7)/9) / √(10) = 2.7508
Calculate the standard error
Standard error = s/√n = 2.7508 / √10 = 0.869
Compute the T-Statistic
t= (x̅ – µ)/ s/√n = (0.7) / 0.869 = 0.805
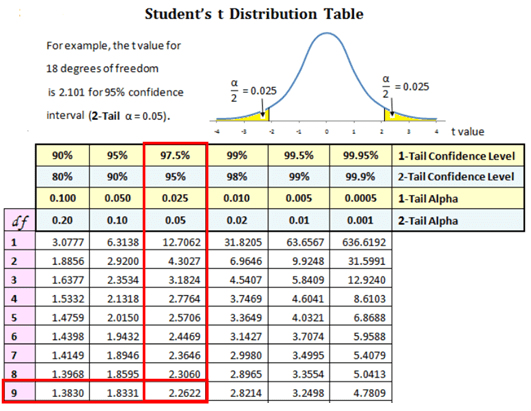
Determine t critical value with n-1 degrees of freedom
Since this is a Two-tailed test at an alpha of 5% t critical = 2.262
Interpret the results
Compare t statistic to t critical 0.805 < 2.262. In Hypothesis Testing, a critical value is a point on the test distribution compared to the test statistic to determine whether to reject the Null Hypothesis. The t calculated is not in the rejection region. Hence, we fail to reject the Null Hypothesis and say there is no difference between the two mean values.
Paired T 2 Tailed Template
Example of One-tailed (Right) Paired t-test
Example: An artificial Intelligence (AI) training institute evaluates the effectiveness of training by comparing the knowledge of the students before and after the execution of live projects. At a 95% confidence level, does this information provide sufficient evidence to indicate that the live projects will improve the students’ AI knowledge?
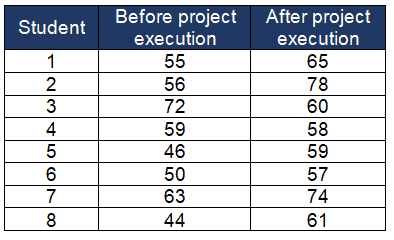
Solution Details:
We need to calculate the T-Statistic value using t = (x̅ – µ)/ s/√n and then compare it to a table value t critical.
- H0 = There is no significant change in AI knowledge before and after the execution of live projects.
- H1 = There is a significant improvement in AI knowledge before and after the execution of live projects.
- n=8
- DF (degrees of freedom) = n-1 ; 8-1 =7
- Significance level =5%
Calculate the difference between each observation in the two groups
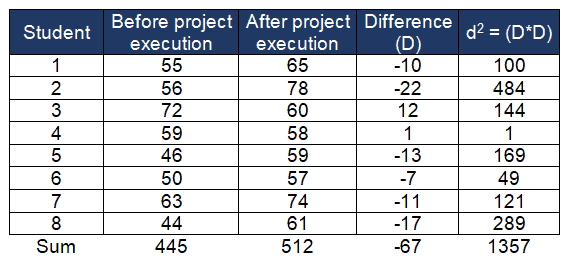
Compute the mean difference (x̅ – µ)
- µ (mean of the first test) = 55.625; take the average of the 8 data points before the project execution
- x̅ (mean of the new test) = 64; take the average of the 8 data points after the project execution
- x̅-µ = 64 – 55.625 =8.375
Calculate the standard deviation of differences (s)
- D= -67 ; d2 = 1357
- Use sd = sqrt [ (Σ(di – d)2 / (n – 1) ] where di is the difference for pair i, d is the sample mean of the differences, or s=( √ ((n*d2)-D2)/df) / √(n)
- s=(√ ((8 * 1357) -(-67 * -67) / 7) / √(8) = 10.66
Calculate the standard error
Standard error = s/√n =10.66 / √8 = 3.769
Compute the T-Statistic
t = (x̅ – µ)/ s/√n = (8.375) / 3.769 = 2.221
Determine t critical value with n-1 degrees of freedom
Since this is a One-tailed (right-tailed) test at an alpha of 5% t critical = 1.8946
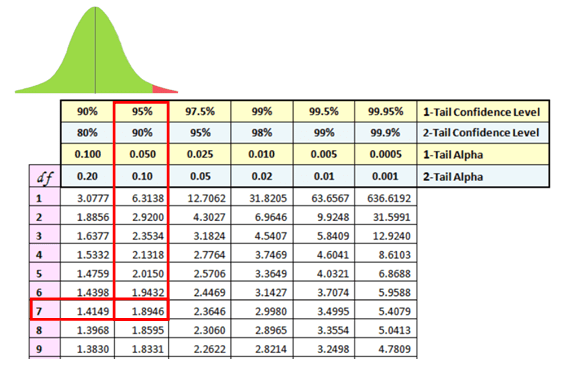
Interpret the results
Compare t statistic to t critical 2.221 > 1.8946. In Hypothesis Testing, a critical value is a point on the test distribution compared to the test statistic to determine whether to reject the null hypothesis. The t calculated is greater than the critical value and is in the rejection region. Hence, we can reject the Null Hypothesis and say that there is a significant improvement in knowledge before and after the execution of live projects.
Paired T Right-Tailed Excel Template
Example of One-tailed (Left) Paired t-test
Example: A dietician evaluates the individual’s weight before and after following the diet plan. At a 95% confidence level, is there any significant evidence of the individuals’ weight reduction?
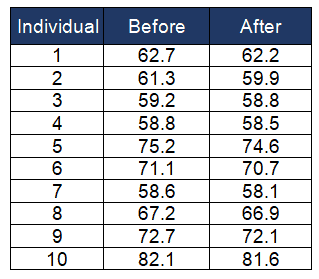
Solution Details:
We need to calculate the T-Statistic value using t= (x̅ – µ)/ s/√n and then compare it to a table value t critical.
- H0 = There is no significant change in weight before and after following the diet plan
- H1 = There is a significant reduction in weight before and after following the diet plan
- n=10
- DF (degrees of freedom) = n-1 ; 10-1 =9
- Significance level =5%
Calculate the difference between each observation in the two groups
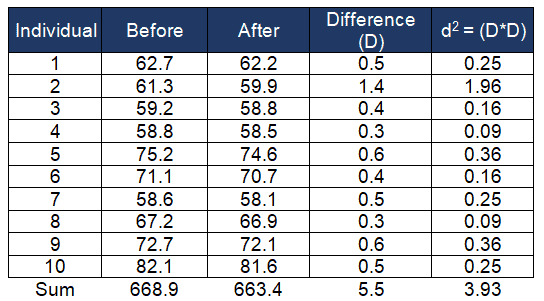
Compute the mean difference (x̅ – µ)
- µ (mean of the first test) = 66.89; take the average of the 10 data points before the diet plan
- x̅ (mean of the new test) = 66.34; take the average of the 10 data points after the diet plan
- x̅-µ = 66.34 – 66.89= -0.55
Calculate the standard deviation of differences (s)
- D= 5.5 ; d2= 3.93
- Use sd = sqrt [ (Σ(di – d)2 / (n – 1) ] where di is the difference for pair i, d is the sample mean of the differences, or s=( √ ((n*d2)-D2)/df) / √(n)
- s=(√ ((10*3.93) -(5.5 * 5.5) / 9) / √(10) = 0.3171
Calculate the standard error
Standard error = s/√n =0.3171 / √10 =0.1002
Compute the T-Statistic
t= (x̅ – µ)/ s/√n = (0.55) / 0.1002 = -5.484
Determine t critical value with n-1 degrees of freedom
Since this is a One-tailed (left-tailed) test at an alpha of 5% t critical = -1.833
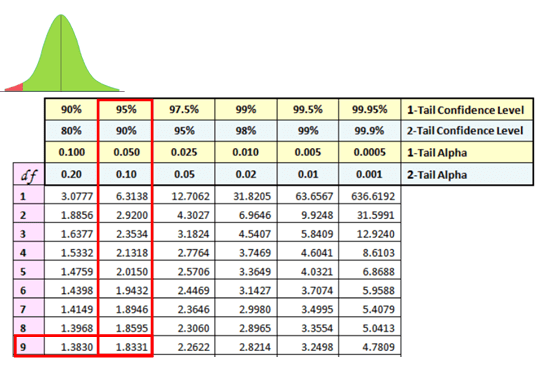
Interpret the results
Compare t statistic to t critical -5.484<-1.833. In Hypothesis Testing, a critical value is a point on the test distribution compared to the test statistic to determine whether to reject the Null Hypothesis. The t calculated is less than the critical value and is in the rejection region. Hence, we can reject the Null Hypothesis and say there is a significant reduction in individual weights before and after the diet plan.
Paired T Left Tailed Excel Template
Important Paired T-Distribution and Paired T-Test Videos
Also, See
ASQ Six Sigma Black Belt Exam Paired Distribution and Paired T-Test Questions
A black belt plans to test the performance of workers before and after training. Which of the following hypothesis tests should be used to determine whether the training actually improved the workers’ performance?
(A) 2-sample z test
(B) 2-sample t-test
(C) Paired t-test
(D) F test
When you’re ready, there are a few ways I can help:
First, join 30,000+ other Six Sigma professionals by subscribing to my email newsletter. A short read every Monday to start your work week off correctly. Always free.
—
If you’re looking to pass your Six Sigma Green Belt or Black Belt exams, I’d recommend starting with my affordable study guide:
1)→ 🟢Pass Your Six Sigma Green Belt
2)→ ⚫Pass Your Six Sigma Black Belt
You’ve spent so much effort learning Lean Six Sigma. Why leave passing your certification exam up to chance? This comprehensive study guide offers 1,000+ exam-like questions for Green Belts (2,000+ for Black Belts) with full answer walkthroughs, access to instructors, detailed study material, and more.


Comments (10)
On the above example, I’m not seeing how you are getting your t-value. Rather than working the Sample Standard Deviation equation s = (Xbar-Mu)/(s/Sqrt of n) are you computing the population std deviation (denominator) by using substuting {Sqrt of (Sum of differences^2/n-1) ]?
Hi Adam,
Thanks for the question. I’ve moved it to the member’s forum and will work it there!
https://sixsigmastudyguide.com/forums/topic/how-to-get-t-value/
Best, Ted.
You use several different t-statistic equations on the answer walkthroughs for the Analyze phase quiz. What are some key words I can look for to determine which equation is applicable?
Also, the standard deviation equation for each t-stat problem in the quiz is different. Could you lead me to some key pointers to look for in deciding which equation is applicable?
Thanks Ted!
Hi Larry,
Timely question. I’m revamping all of the T-based statistics supplementary material now. I’ll certainly incorporate your thoughts – thanks!
In short, the analyze phase quiz tests multiple types of T-statistic questions(One Sample, Two Sample, Paired, Students). For each of these there are ways to decide which one to use. I’ll be sure to call that out. The Hub page for all of the different types of questions will be here: T Distributions and Calculations.
For standard deviation, remember that you calculate it differently depending upon if you are using a sample or an entire population. See more here Standard Deviation
Best, Ted.
Hi Ted,
The link to the cliffnote does not work. I wonder if you could update the source?
Best,
Qian
Hi Qian,
We’ve done the next best thing and completely re-written the article from top to bottom. What do you think?
Best, Ted.
Hi Ted,
I tried both formulas and ended up with different answers. Can you kindly explain the difference in these formulas:
Use sd = sqrt [ (Σ(di – d)2 / (n – 1) ] where di is the difference for pair i, d is the sample mean of the differences, or s=( √ ((n*d2)-D2)/df) / √(n)
much appreciated
edward
Hi Ed,
Your first equation is standard deviation of a sample. You can see more here in my article on standard deviation.
Can you give me more context where you’re seeing the second equation?
Best, Ted
The IASSC reference doc is full of errors when it comes to the different formulas to calculate t. For paired t test for example, it uses D bar instead of x̅ – µ.
t= (x̅ – µ)/ s/√n
where x̅ = mean of new test and µ = mean of first test
This may for some questions – such as the one about operator error above – get the correct absolute value, but the wrong sign, e.g. x̅ – µ = 0.7, while D bar is -0.7.
The 2 sample t-test unequal variance formula is also incorrect, it shows an unnecessary extra square root.
I only just noticed the first issue but had already contacted IASSC several weeks ago about the 2 sample t-test formula. A case file was opened but there has been no further update since.
Yes Wiebke Zuch, we also believe the formulas referenced on the IASSC page are inaccurate. Hence, we update the correct formula. Please see the below reference links
https://sixsigmastudyguide.com/green-belt-answers/green-belt-analyze-answers/2-sample-t-test-for-means-unequal-variance-answers/
Thanks