1 sample Wilcoxon non parametric hypothesis test is one of the popular non-parametric tests. One sample t-test is to compares the mean of the population to the known value (i.e more than, less than, or equal to a specific known value). The t-test always assumes that random data and the population standard deviation is unknown.

Wilcoxon Signed-Rank test is the equivalent non-parametric t-test, and this may be used when the dependent variable is not normally distributed. The Wilcoxon signed test is designed to test hypotheses about the location (median) of a population distribution.

History

The Wilcoxon signed test was first developed by Frank Wilcoxon, an American chemist in the year 1945, but popularized by Sidney Siegel in 1956. Wilcoxon Signed test can be used for a single sample, matched paired data (example before and after data), and also for unrelated samples ( it is almost similar to Mann Whitney U test).

Disambiguation

1 sample Wilcoxon non parametric hypothesis test is a rank-based test and it compares the standard value (theoretical value) with the hypothesized median. Usually, the t-test depends on the sample mean which is not so stable in heavy-tailed distribution; hence Wilcoxon test efficiency is high when compared to the t-test.

The name Sign test and Wilcoxon signed ranked test look similar and both are used for one sample & two samples, but Wilcoxon signed rank test is more powerful than the signed test.

Wilcoxon Signed-Rank Test for Paired Samples – This test is mainly an alternative to the t-test for paired samples i.e. if the requirements for the two paired t-tests are not satisfied then we can easily perform this test. It has three requirements all of which should be satisfied in order to perform this test. It has two methods: the exact one and the advanced one.

Hypothesis of 1 sample Wilcoxon Signed test

Left-tailed test:

• Null Hypothesis H₀: The population median (η) is greater than or equal to hypothesized median(η₀)- η≥ η₀
• Alternative Hypothesis : H₁: The population median(η) is less than the hypothesized median(η₀) – η<η₀

Right-tailed test:

• Null Hypothesis H₀: The population median (η) is less than or equal to hypothesized median(η₀)- η≤η₀
• Alternative Hypothesis : H₁: The population median(η) is greater than the hypothesized median(η₀)- η>η₀

Two-tailed test:

• Null Hypothesis H₀: The population median (η) is equal to hypothesized median(η₀)- η=η₀
• Alternative Hypothesis : H₁: The population median(η) is not equal to the hypothesized median(η₀)- η≠η₀

Assumptions of the one sample Wilcoxon test

• Differences between the data value and the hypothesized median are continuous
• Data follows the symmetric distribution
• Observations are mutually independent of each other
• Measurement scale is at least an interval

Procedure to execute One Sample Wilcoxon Non Parametric Hypothesis Test

• Identify the difference between each individual value and the median
• If the difference between the individual value and the median is zero, ignore it.
• Ignore the signs of the different values and assign the lowest rank to the smallest difference value. If the values have been tied, then consider the mean value.
• Compute the sum of ranks of positive difference values, and negative difference values (W+ and W-)
• If the values are (>20), the normal approximation would be

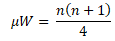
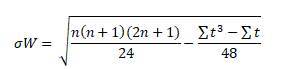
Where t is the rank of tied values

• Calculate the z-value using

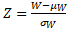
• Compare the test statistic, W, with the critical value in the tables; the null hypothesis can be rejected if W is less than or equal to the critical value.
• Now, compare the test statics with critical values in the tables and make a decision, the null hypothesis will be rejected if the test statistic, W, is less than or equal to the critical value
• Interpret the decision in the context of the original claim.

Example of One Sample Wilcoxon Test

In a law college, random samples of 10 students’ marks are noted below, is there evidence at the 5% confidence level to suggest that the median mark is greater than 67?

• Null Hypothesis H₀: The population median value ≤ 67 marks
• Alternative Hypothesis : H₁: The population median value > 67 marks

Ignoring the signs, rank the differences smallest rank =1

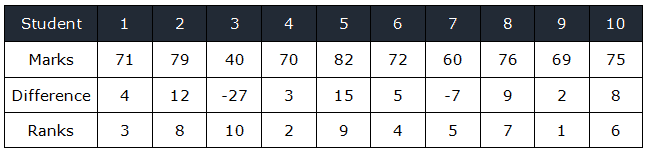
Separate the positive and negative ranks

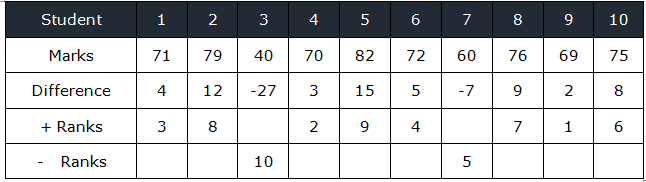
• Sum of + ranks =40
• Sum of – ranks=15
• Smallest value among 40 & 15 =15
• Test statistics =15

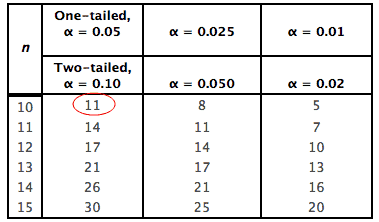
Critical value =11

The null hypothesis will be rejected if the test statistic, W, is less than or equal to the critical value.

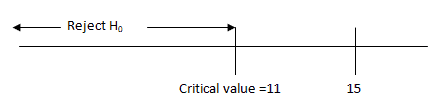
Since the test statistic value is greater than the critical value, hence we fail to reject the null hypothesis. There is no significant evidence that the median rank is greater than 67.

Additional Wilcoxon Examples and Helpful Links:

http://www.unm.edu/~marcusj/WilcoxonSR.pdf

Six Sigma Black Belt Certification 1 Sample Wilcoxon Test Questions:

Question 1:  Which of the following scenario the decision will impact the Wilcoxon test?

(A) Ties the values between the samples
(B) Ties of values never impact the decision
(C) Ties values within one sample
(D) Ties the values always impact the decision

Answer C:   Ties the values within one sample impacts the decision of the Wilcoxon test, hence If the values have tied, then consider the mean value.