Attribute Chart: u Chart

What is a u Chart?

Attribute chart: u chart is also known as the control chart for defects per unit chart. It is generally used to monitor the count type of data where the sample size is greater than one. There may be a single type of defect or several different types, but the u chart tracks the average number of defects per unit, and it assumes the underlying data approximate the Poisson distribution.

With u charts, the number of defects per single unit is plotted on the y-axis, and the number of units or lots is on the x-axis. The centerline (u̅) is the total number of defects in a sample divided number of inspected items in a sample.

Selection of Control chart

The control chart is a graph used to study how a process changes over time. A control chart always has a central line for the average, an upper line for the upper control limit, and a lower line for the lower control limit. The control limits are ±3σ from the centerline.

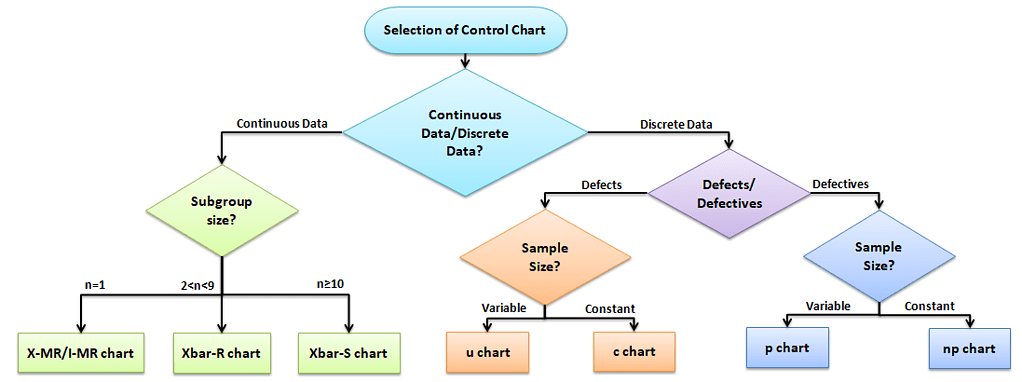
Selection of an appropriate control chart is very important in control charts mapping, otherwise ended up with inaccurate control limits for the data.

X̅ and R charts are used for measurable quantities such as length, weight, and height.  Attribute control charts are used for attribute data.  In other words, the data that counts the number of defective items or the number of defects per unit. For example, the number of tubes failed on a shop floor. Unlike variable charts, only one chart is plotted for attributes.

Why and When do you use a u Chart?

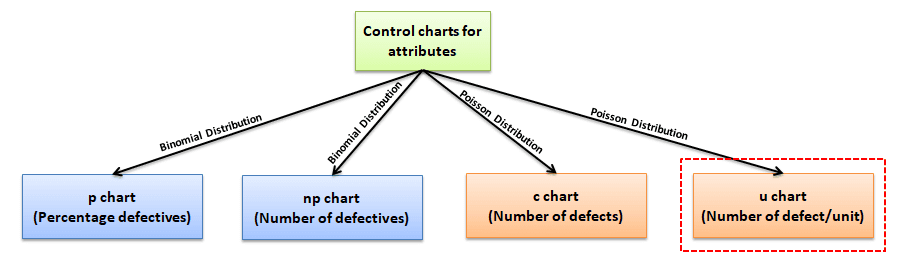
u chart is one of the quality control charts to monitor the number of defects per unit, while the c chart is for a constant sample size.

Use a u chart to monitor process stability over time and monitor the effects of before and after process improvements. It is used when the sample size varies, such as the number of meals, bills delivered each day, etc. It computes control limits based on the Poisson distribution.

Four types of control charts exist for attribute data. p chart plots the proportion of defective items, and the np chart is for the number of defectives.  c chart is for the number of defects, and the u chart is for the average number of defects per unit.

Assumptions of Attribute charts: u chart

• The probability of defect is the same for each item
• Each unit is independent of the other
• The testing procedure should be the same for each lot

How do you Create a u Chart

• Determine the subgroup size. The subgroup size must be large enough for the c chart; otherwise, control limits may not be accurate when estimated from the data.  
• Count the number of defects in each inspected unit.
• Calculate u value for each lot u= number of defects in each lot/ lot size.
• Compute centreline u̅= total number of defects / total number of samples =Σc/Σn.
• Calculate the upper control limit (UCL) and low control limit (LCL). If the sample sizes are unequal, the control limits vary from sample interval to sample interval.
• Plot the graph with the number of defects per unit on the y-axis, and lots on the x-axis: Draw the centerline, UCL, and LCL. Use these limits to monitor the number of defects going forward.
• Finally, interpret the data to determine whether the process is in control.

Attribute Chart: u chart formulas (variable sample size)

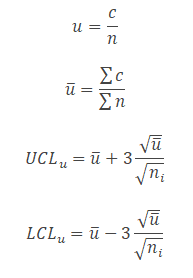
• Where c = number of defects
• K= number of lots
• n= sample size

Example of using a u Chart in a Six Sigma project (variable sample size)

Example: A motorbike manufacturer collected the number of defects identified in the final inspection stage for 20 days. Based on the given data, the supervisor wants to know the quality level using a control chart for defects per motorbike and determine the process in statistical control.

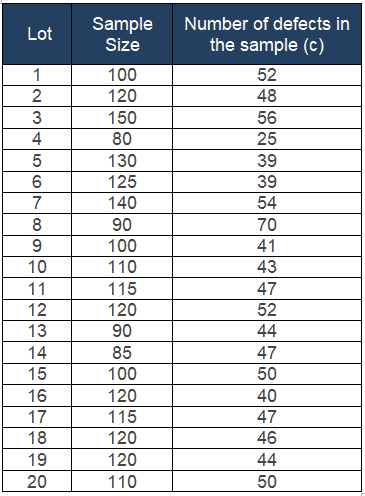
• no of lots k = 20
• Sum of defects Σc = 934
• Sum of sample size Σn = 2240

Calculate the u value for each lot; u= number of defects in each lot/ lot size

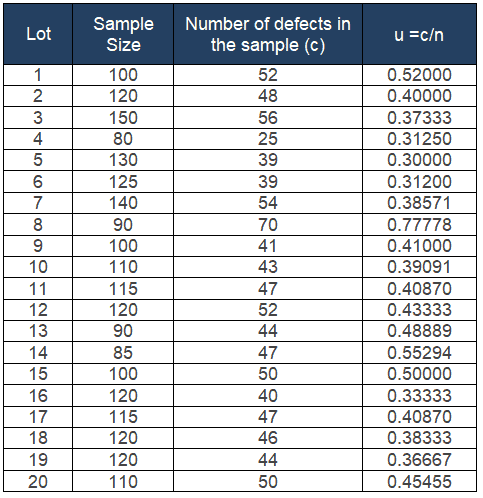
Compute u̅ = total number of defects / number of samples =Σc/Σn

=934/2240= 0.417

Then calculate the upper control limit (UCL) and low control limit (LCL). Since the sample sizes are unequal, the control limits vary from sample interval to sample interval.

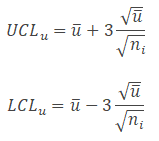
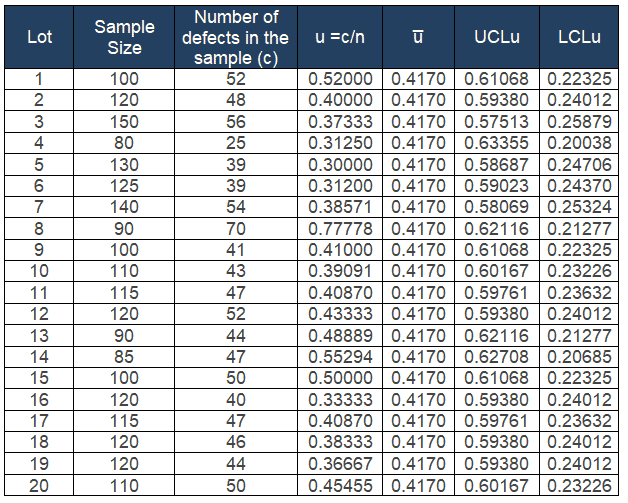
Plot the graph with defects per single unit on the y-axis and lots on the x-axis, and also draw a center line (u̅), UCL, and LCL.

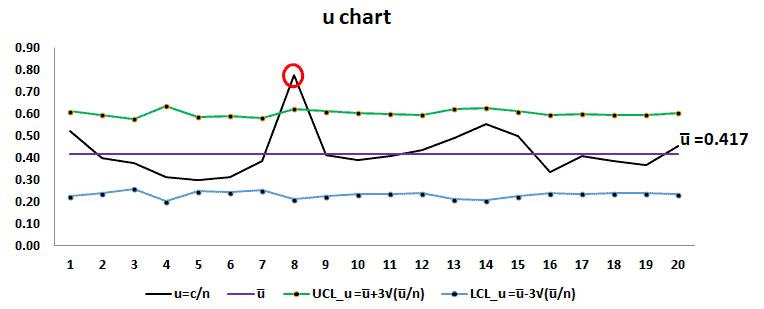
Interpret the chart: If any of the points in the chart are outside of ± 3σ limit, then consider the process is out of control. In the above example, Sample 8 is outside of the control limit. Hence the process is not in control. Thus, the team needs to identify the root cause for the special cause variation.

Attribute Chart: u chart formulas (constant sample size)

u chart considers the average number of defects per unit, while the c chart analyzes the number of defects in a given sample. We can use the following method to compute an average number of defects per unit chart if all the samples are the same size.

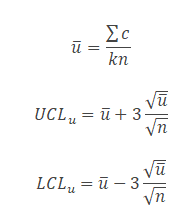
• Where c = number of defects
• K= number of lots
• n= sample size

Example of using a u Chart in a Six Sigma project (constant sample size)

Example: The following data shows the number of defects per lot in 20 consecutive lots of 100 motorbikes each. Plot the average number of defects per unit based on the data and determine the process in statistical control.

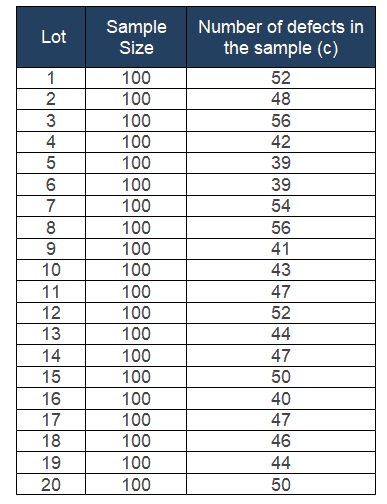
• no of lots k = 20
• Sum of defects Σc = 937
• Sum of sample size n = 100

Calculate the u value for each lot; u= number of defects in each lot/ lot size

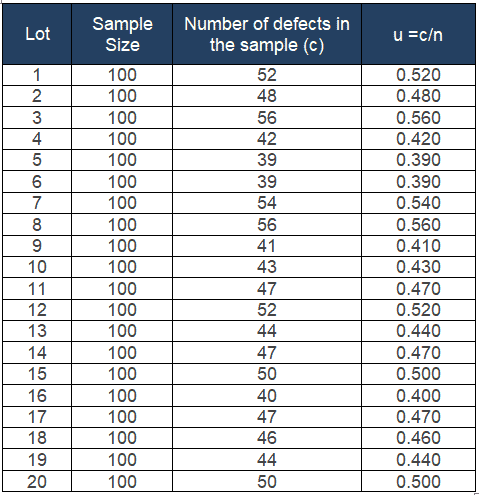
Compute u̅ = =Σc/nk =937/(20*100) = 0.4685

Then calculate the upper control limit (UCL) and low control limit (LCL).

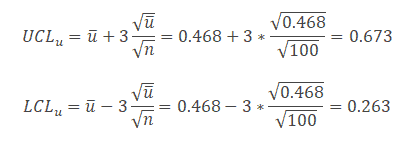
Plot the graph with defects per single unit on the y-axis, and lots on the x-axis, and also draw a center line (u̅), UCL, and LCL.

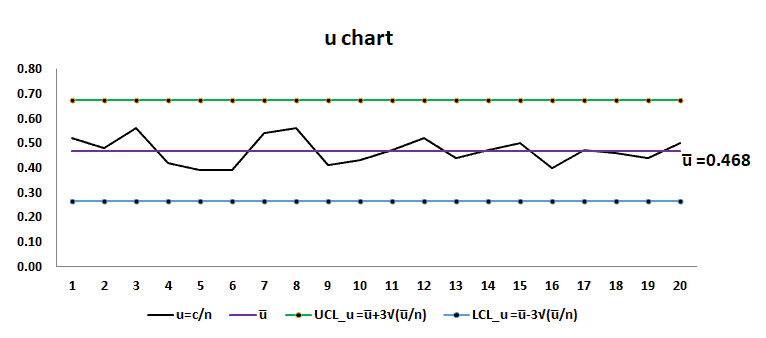
Interpret the chart: If any of the points in the chart are outside of ± 3σ limit, then consider the process is out of control. In the above example, all the samples are within the control limit. Hence we assume the process is in control.

U Chart Template Download

Videos of u Charts

Additional Helpful Links

https://www.six-sigma-material.com/U-Chart.html

https://ncss-wpengine.netdna-ssl.com/wp-content/themes/ncss/pdf/Procedures/NCSS/U_Charts.pdf

https://www.spcforexcel.com/knowledge/attribute-control-charts/small-sample-case-for-c-and-u-control-charts