Non-parametric tests, as their name tells us, are statistical tests without parameters. For these types of tests, you need not characterize your population’s distribution based on specific parameters. Non-parametric tests are also referred to as distribution-free tests due to the fact that they are based n fewer assumptions (e.g. normal distribution).
“This always reminds me of the Ghostbuster’s scene when they get their first call and head into the hotel where the manager says ‘I want this thing taken care of quickly!’ Venkmann of course replies ‘Hold on, we don’t even know what you have yet.’”
Parametric tests involve specific probability distribution and the tests involve estimation of the key parameters of that distribution. Whereas, non-parametric tests are particularly for testing hypotheses, whose data is usually non-normal and resists transformation of any kind. Due to the lesser amount of assumptions needed, these tests are relatively easier to perform. They are also more robust.
When to use Non-parametric testing?
Non-parametric methods can be used to study data that are ranked in order but has no or little clear numerical interpretation.
Due to the small number of assumptions involved, non-parametric tests have a wide range of applications, especially where there is only a small amount of information available about the application in question.
For data to give you reliable results with non-parametric tests it should not follow a normal distribution. A common test to check that is the Anderson-Darling Test which helps us determine the type of distribution the data may follow. Perform a non-parametric test, If the test result is statistically significant and the data does not follow a normal distribution.
Perform non-parametric tests easily where some of the situations when the data is not following a normal distribution:
- When the outcome is a rank or an ordinal variable – For example in the case of movie ranking etc.
- In case there are a number of explicit outliers – The samples may show a continuous pattern with some very extreme-ended outliers.
- When the outcome has a clear limit of detection – This means that the outcome has with some limitations or imprecision.
Applications of Non-parametric tests
- When data does not follow parametric test conditions
- Where you need quick data analysis
- Whose data is usually non-normal and resists transformation of any kind.
- When the sample size is too small
Assumptions of Non-parametric tests
Usually, we don’t assume that the data is following the normal distribution while we are performing the nonparametric test; however, that does not mean we don’t have any assumption about the non-parametric test.
- Samples are independent and derived from the same population
- Need to have an equal shape and spread for two sample designs
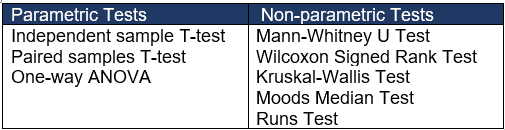
Types of Non-parametric Tests
There are many types of non-parametric tests. The following are a few:
Sign Test – It is a rudimentary test that can be applied when the typical conditions for the single sample t-test are not met. The test itself is very simple and involves doing a binomial test on the signs.
Mood’s Median Test (for two samples) – This is a rudimentary two-sample version of the above-mentioned sign test. It is to estimate whether the median of any two independent samples is equal. This test can be applied to more than two samples.
Wilcoxon Signed-Rank Test for a Single Sample – If the requirements for the t-test are not fulfilled then this test can be used only if the two dependent samples to be used have been derived from populations with an ordinal distribution. This is also a rudimentary test. It has two subtypes: the exact test and the advanced one.
Mann-Whitney Test for Independent Samples – This is also an alternative version of the t-test for two independent populations. This test is completely equivalent and resembles the Wilcoxon test in some ways. This test has three types: the exact test, the median confidence interval, and the advanced one.
Wilcoxon Signed-Rank Test for Paired Samples – This test is mainly an alternative to the t-test for paired samples i.e. if the requirements for the two paired t-tests are not satisfied then we can easily perform this test. It has two methods: the exact one and the advanced one.
McNemar Test–
This test is basically a type of matched pair test and is used to analyze data before and after an event has occurred. It tells us whether there is a significant change in the data before and after the occurrence of any said event. Use McNemar’s Test with paired samples where the dependent variable is dichotomous.
Runs Test – This test is to determine whether the sequence of a series of events is random or not. Use one or two sample types depending on the data available at hand and the resources available. The two-sample test determines whether the two samples come from the same distribution of data or not.
Resampling Procedures – Works on the assumption that the original population distribution is the same as in the given sample. This helps us create a large number of samples from this pseudo-population and then in end draw valuable conclusions.
Additional Non-Parametric Hypothesis Tests
Apart from the above non-parametric test, some of the other examples of non-parametric tests used in our everyday lives are the Chi-square Test of Independence, Kolmogorov-Smirnov (KS) test, Kruskal-Wallis Test, Mood’s Median Test, Spearman’s Rank Correlation, Kendall’s Tau Correlation, Friedman Test and the Cochran’s Q Test.
Also, see one and two sample proportion non-parametric hypothesis tests, 1 Sample Sign Non Parametric Hypothesis Test,
Advantages of Non-parametric tests
- Non-parametric tests are distribution free
- An added advantage is the reduction in the effect of outliers and variance heterogeneity on our results.
- It can be applied to nominal (such as sex, race, employment status, etc.) or ordinal scaled data ( on a 1-10 scale, 10 being delighted and 1 being extremely dissatisfied)
- Computations are easier than the parametric test
- Easy to understand and less time-consuming especially when the sample size is small
Disadvantages of Non-parametric tests
- The results that they provide may be less efficient or powerful compared to the results provided by the parametric tests.
- Non-parametric tests are useful and important in many cases, but it is difficult to compute manually.
- Results are usually more difficult to interpret than parametric tests
Notes:
- Use Non-parametric tests for correlation studies
- Tests for equality of population medians – Mood’s Median, Mann Whitney, and Kruskal Wallis
- Non-Parametric Test of equality of population variances – Levene’s Test
- Levene’s test – makes an evaluation using a t-test http://en.wikipedia.org/wiki/Levene’s_test (Levene’s test of equal variances)
Non-Parametric test videos
Six Sigma Black Belt Certification Non-Parametric Tests and Data Analysis Questions:
Question: A black belt would use non-parametric statistical methods when:
(A) knowledge of the underlying distribution of the population is limited
(B) the measurement scale is either nominal or ordinal
(C) the statistical estimation is required to have higher assurance
(D) management requires substantial statistical analysis prior to implementing
Answer:
A: knowledge of the underlying distribution of the population is limited.
You use non-parametrics when you can’t identify or assume what kind of distribution you have so A is the easy choice. Also, you can eliminate b, c, and d as they have no bearing on the problem.


Comments (4)
Hi,
I would believe the correct answer is B not A.
I can run a normality test to know if the data follow normal distribution or not, and that’s enough information to whether use non-parametric statistical methods.
However if the measurement scale is either ordinal or nominal, then by definition I have to use non-parametric statistical methods.
Thanks,
Ahmed
Hi Ahmed,
Thanks for the question. This question comes from ASQ’s published practice exam and that is their provided answer.
I think it comes down to which is the best possible answer. While you are right in terms of B, A is the better answer as it is more encompassing.
Best, Ted
Hi Nikil,
Thanks for reaching out. I moved this conversation to the private member’s forum. I’ll follow up there.
As a reminder, please only discuss the questions from the practice exams in the member’s forum.
Best, Ted.