Mann-Whitney Non Parametric U Test

The preferred non-parametric method for unpaired samples is the Mann-Whitney non parametric hypothesis test or Mann-Whitney test (it is also called as Wilcoxon Rank Sum Test or the Mann-Whitney Wilcoxon Test) and thus the non parametric solution to evaluating two independent datasets comparable to the Student’s T-test.

The Mann-Whitney U test is a non-parametric statistical test used to compare two independent samples. It assesses whether the distribution of values in one sample is stochastically greater or less than the distribution of values in another sample. This test does not specifically compare sample means, but rather it evaluates whether the two samples come from the same population or if one tends to have higher values than the other.

A few researchers also interpret the Mann-Whitney test will help to compare the medians of the two populations. Usually, parametric tests will compare the means (Null hypothesis: μ1=μ2) between the independent groups. Whereas, the null hypotheses and the two-sided hypotheses non-parametric tests can be indicated as follows:

• Null Hypotheses H₀: Two populations are equal
• Alternative Hypotheses H₁: Two populations are not equal.

The Mann-Whitney test is regularly performed as a two-sided test, therefore the investigative hypothesis indicates that the two populations are not equal, instead of specifying the directionality.

Assumptions of the Mann-Whitney:

• The sample drawn from the population is random.
• Independence within the samples and also mutual independence is assumed.  That means that an observation is in one group or in the other (it cannot be in both).
• Identical (non-normal) distributions
• An Ordinal measurement scale is assumed.

Uses of Mann-Whitney

Mann-Whitney U test is can be used for every industry. But is more frequently used in healthcare, nursing, business, and also many other disciplines.  In medicine, it is a more efficient method to know the effect of two medicines and whether they are equal or not.  It is also used to know whether or not a particular medicine cures an ailment or not. 

Procedure to conduct Mann-Whitney test

• Combine two samples of data together, and sort the data in ascending order
• Convert data to ranks (1, 2, 3,… Y)
• Separate ranks back into two samples
• Compute the test statistic, U
• Determine the critical value of U from the Mann-Whitney table
• Finally, Formulate a decision and conclusion

Calculation of Mann-Whitney Test

Case 1: For comparing two small sets of observations (samples sizes less than 20)

U₁ = n₁n₂+0.5n₁(n₁+1)-R₁

U₂ = n₁n₂+0.5n₂(n₂+1)-R₂

Where U₁+U₂=n₁n₂

• n₁ is the observations from the first population
• n₂ is the observations from the second population
• R₁ is the sum of observation ranks for the first population
• R₂ is the sum of observation ranks for the second population

Finally, calculate the U statistic as the smaller U₁ and U₂. U= min (U_1, U₂)

Case2: Normal approximation and tie correction

For sample sizes above ~20, the distribution of U rapidly approaches the normal distribution

U mean = μ_U =0.5 n₁n₂

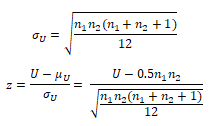
Example of Mann-Whitney Test

A researcher, while conducting studies on the Biomass of various trees, wished to determine if there was a difference in the biomass of male and female Juniper trees. So, he randomly selected 6 individuals of each gender from the field. He dries them to constant moisture, chips them, and then weighs them to the nearest kg.

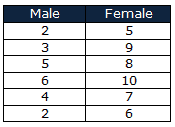
• H₀: There is no difference between the biomass of male and female Juniper trees– Biomass_male = Biomass_female (medians are equal)
• H₁: There is a difference between the biomass of male and female Juniper trees– Biomass_male ≠ Biomass_female (medians are not equal)

The data are ratings (ordinal data), and hence a non-parametric test is appropriate – the Mann-Whitney U test (the non-parametric counterpart of an independent measures t-test).

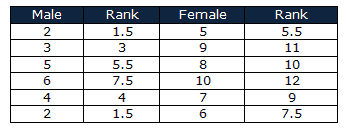
• n₁ =6
• n₂ =6
• R₁ = 1.5 + 3 + 5.5 + 7.5 + 4 + 1.5 = 23
• R₂ = 5.5 + 11 + 10 + 12 + 9 + 7.5 = 55

And then calculate U₁ and U₂

• U₁ = n₁n₂+0.5n₁(n₁+1)-R₁ = 6 *6 + 0.5 * 6(7) – 23 = 34
• U₂ = n₁n₂+0.5n₂(n₂+1)-R₂ = 6 * 6 + 0.5 * 6(7) – 55 = 2

U= min (U_1, U₂) = 2

Mann-Whitney Table: For Two-Tailed Test at a 5% Significance Level

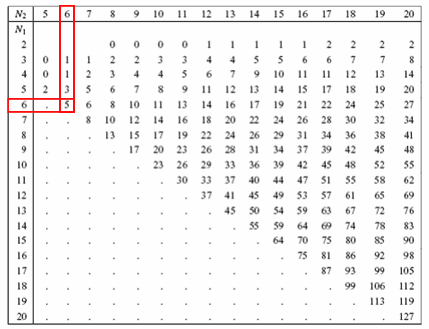
U_critical = 5

Calculated U is a value less than the critical value of U for a 0.05 significance level. U_calculated < U_critical . Hence, we can reject the null hypothesis.

So, we can say there is a highly significant difference between male and female Juniper trees’ biomass.

Six Sigma Black Belt Certification Mann-Whitney Test Questions:

Question: Which of the following test is calculated by ranking all the participant’s scores from lowest to highest and adding up the ranks separately for each of the groups?

(A) Wilcoxon signed rank test
(B) Kruskal Wallis test
(C) Mann-Whitney test
(D) Friedman Test

Answer:

C. In the Mann-Whitney test, combine two data sets and then arrange the observations in ascending order. Rank the two groups, similarly if it ties average their rank numbers.