Mood’s median test is a nonparametric test to compare the medians of two independent samples. It is also used to estimate whether the median of any two independent samples is equal. Therefore, Mood’s median non parametric hypothesis test is an alternative to the one-way ANOVA. This test works when the dependent variable is continuous or discrete count, and the independent variables are discrete with two or more attributes.

Mood’s median test is a rudimentary two-sample version of the sign test. This test can be applied to more than two samples, but it is not as powerful as Kruskal-Wallis Test.

While Mood’s median test is more useful for smaller sample sizes when the data contains few outliers because this test only focuses on median value instead of ranks.

Usually, the researchers prefer the Wilcoxon Rank Sum test or Mann-Whitney U test as they provide more robust results when compared to Mood’s Median Test.

The Mood’s median test compares whether K-independent samples have either drawn from the same population or from populations with equal medians.

Assumptions of the Mood’s Median Test

• The Observations are independent both within and between samples.
• The Observations come from a population with a continuous distribution function
• The distributions of the populations the samples were drawn from all have the same shape.

Uses of Mood’s Median Test

Following are a few examples where Mood’s median test can be used:

• The Moods median test is to compare the medians of customer satisfaction level (dependent variable) of different account holders (independent variables: current account and savings account customers).
• To compare the medians of machining times of different production lines in a manufacturing plant (Lines 1, 2, and 3 )

Procedure to execute Mood’s Median Non Parametric Hypothesis Test

• Compute the overall median (M) of the combination of k samples—list all the data into a single set and sort the data into ascending order, finally find the middle number (median M)
• Count the number of observations that is greater than the overall median (M), and then count the observations that are equal to or less than the median (M).
• Create a 2xk contingency table with the above data
• Compute the chi-square test for the completed contingency table
• Compare the calculated value with the chi-square critical value
• Finally, formulate a decision and conclusion

Calculation of Mood’s Median Test

The Mood’s Median Test is used to determine whether there is sufficient evidence to conclude that samples are drawn from populations with different medians. The test statistic used is the chi-square test statistic

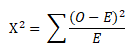
Where O is Observed Frequency and E is the Expected Frequency

• Null Hypothesis H₀: The medians of the populations all are equal
• Alternative Hypothesis H₁: The medians of the population are not all equal (at least one population median is different)

DF= (rows-1)*(columns-1)

Example of Mood’s Median Non Parametric Hypothesis Test

A major wheat supplier from Texas is analyzing the yields of various crop methods. He randomly assigned two different wheat crop methods to a very high number of different acres of farmland and recorded the production rate (yield per acre) for each plot.

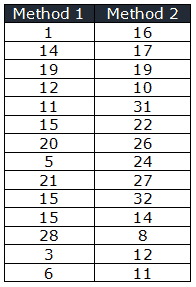
Step 1: Calculate the total median from two methods. First sort the data into ascending order and find the middle number

1,3,5,6,8,10,11,11,12,12,14,14,15,15,15,16,17,19,19,20,21,22,24,26,27,28,31,32

Overall Median = 15 + 15 / 2 = 15

Step 2: Create a 2X2 contingency table from the above values

Step 3: Perform Chi-square (χ²) test

Observed Frequencies :

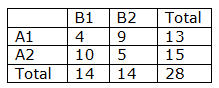
Expected Frequencies :

Expected value for each cell= row total * column total/grand total

(A) Cell (A1XB1) = 14 * 13 / 28 = 6.5
(B)  Cell (A2XB1) = 14 * 15 / 28 = 7.5
(C) Cell (A1XB2) = 14 * 13 / 28 = 6.5
(D) Cell (A2XB2) = 14 * 15 / 28 = 7.5

Step 4: Compute the degrees of freedom = (2 – 1) * (2 – 1) = 1

Critical value of χ² (0.05, 1) = 3.841

Step 5: Calculated χ² value is less than the critical value of χ² for a 0.05 significance level, hence we have no convincing evidence to reject the null hypothesis

So, the data are consistent with the null hypothesis that there is no difference between the two wheat crop methods.

Six Sigma Black Belt Certification Mood’s Median Test Questions:

Question: What statistical test would be used to compare medians of two independent samples?

A) Wlcoxon Ranked Sum test
(B) Mann-Whitney U test 
(C) Mood’s Median test
(D) All the above

Answer:

C:  Moods Median test compares the medians of two independent samples, whereas the Wilcoxon and Mann–Whitney test takes the ranks of each observation into account.