Kruskal-Wallis Test

The Kruskal–Wallis Non Parametric Hypothesis Test (1952) is a nonparametric analog of the one-way analysis of variance. It is generally used when the measurement variable does not meet the normality assumptions of one-way ANOVA. It is also a popular nonparametric test to compare outcomes among three or more independent (unmatched) groups.  

Consider the Mann–Whitney test for just two groups instead of the Kruskal–Wallis test. Like the Mann-Whitney test, this test may also evaluate the differences between the groups by estimating the differences in ranks among the groups.

Generally in the ANOVA test, the assumption is that the dependent variable is drawn from a normally distributed population and also assumes that common variance across groups.  But, in Kruskal-Wallis Test, there is no necessity for these assumptions. Therefore, this test is the best option for both continuous as well as ordinal types of data.

Assumptions of the Kruskal-Wallis Test

• All samples are randomly drawn from their respective population.
• Independence within each sample.
• The measurement scale is at least ordinal.
• Mutual independence among the various samples

Uses of Kruskal-Wallis Non Parametric Hypothesis Test Test

The Kruskal-Wallis test can be used for any industry to understand the dependent variable when it has three or more independent groups. For example, this test helps to understand the student’s performance in exams. While the scores are measured on a scale from 0-100, the scores may vary based on the exam anxiety levels (low, medium, high, and severe -in this case, four different groups) of the students.

Procedure to conduct Kruskal-Wallis Test

• First pool all the data across the groups.
• Rank the data from 1 for the smallest value of the dependent variable and the next smallest variable rank 2 and so on… (if any value ties, in that case, it is advised to use mid-point), N being the highest variable.
• Compute the test statistic
• Determine critical value from the Chi-Square distribution table
• Finally, formulate a decision and conclusion

Most of the teams lose track when they exercise the ranks for the original variables. Hence this can make Kruskal–Wallis test a bit less powerful than a one-way ANOVA test.

Calculation of the Kruskal-Wallis Non Parametric Hypothesis Test

The Kruskal–Wallis Non Parametric Hypothesis Test compares medians among k groups (k > 2). The null and alternative hypotheses for the Kruskal-Wallis test are as follows:

• Null Hypothesis H₀: Population medians are equal
• Alternative Hypothesis H₁: Population medians are not all equal

As explained above, the procedure for the Kruskal-Wallis test pools the observations from the k groups into one combined sample, and then ranks from lowest to highest value (1 to N), where N is the total number of values in all the groups.

The test statistic for the Kruskal Wallis test (mostly denoted as H) is defined as follows: 

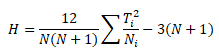
Where T_i = rank sum for the ith sample i = 1, 2,…,k

In the Kruskal-Wallis test, the H value will not have any impact on any two groups in which the data values have the same ranks. Either increasing the largest value or decreasing the smallest value will have zero effect on H.  Hence, the extreme outliers (higher and lower sides) will not impact this test.

Example of Kruskal-Wallis Non Parametric Hypothesis Test

In a manufacturing unit, four teams of operators were randomly selected and sent to four different facilities for machining techniques training. After the training, the supervisor conducted the exam and recorded the test scores. At 95% confidence level does the scores are same in all four facilities?

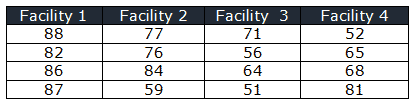
• Null Hypothesis H₀: The distribution of operator scores are same
• Alternative Hypothesis H₁: The scores may vary in four facilities

Rank the score in all the facilities

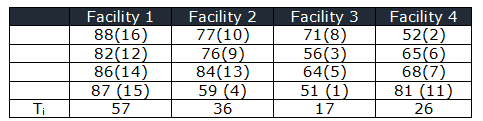
N=16

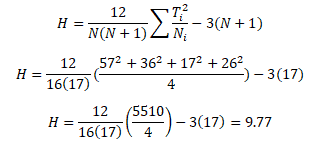
While for a right-tailed chi-square test with a 95% confidence level, and df =3, the critical χ² value is 7.81

Critical values of Chi-Square Distribution

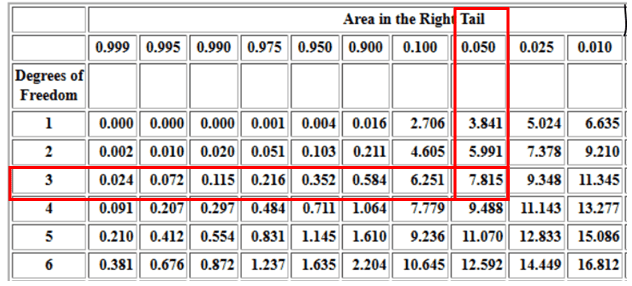
The calculated χ² value is greater than the critical value of χ²for a 0.05 significance level. χ²_calculated >χ²_critical hence, you reject the null hypotheses

So, there is enough evidence to conclude that difference in test scores exists for four teaching methods at different facilities.

Six Sigma Black Belt Certification Kruskal-Wallis Test Questions:

Question 1: In an organization, management conducted a study comparing Purchase, Marketing, Quality, and Production groups on a measure of leadership skills. Which of the following test would an organization choose?

(A) Mood’Median test
(B) Kruskal-Wallis test
(C) Mann-Whitney U test
(D) Friedman Rank Test

Answer B: It is independent data and there are more than two conditions, hence Kruskal-Wallis test is the best option.

Question 2: Which of the following nonparametric test use the rank sum?

(A) Runs test
(B) Mood’Median test
(C) Sign test
(D) Kruskal-Wallis test

Answer D: Kruskal-Wallis test pools the observations from the k groups into one combined sample, and then ranks from lowest to the highest value.