Chi square goodness of fit test specifically tells how well a categorical (nominal or ordinal) sample distribution fit into a hypothetical distribution. In other words, it is the test used to check if the sample data is consistent with a hypothesized distribution of the population. The goodness of fit test is used to determine the observed sample distribution matches or fits the expected values; hence we use the term goodness of fit.

The goodness of fit is a non-parametric test because it does not rely on estimates of a population parameter like mean or variance to make an inference on the characteristics of the population.

When to use Chi Square Goodness of Fit?

A chi-square goodness-of-fit test can be conducted when there is one categorical variable with more than two levels. If there are exactly two categories, then a one proportion z test may be conducted.

Reference.

The chi-square goodness-of-fit test requires 2 assumptions^2,3:

1. independent observations;

2. for 2 categories, each expected frequency EiEi must be at least 5.

For 3+ categories, each EiEi must be at least 1 and no more than 20% of all EiEi may be smaller than 5.

Reference

Structure of a Chi Square Goodness of Fit Test

The Goodness of fit tests are structured in cells; therefore, the observed frequency goes in each cell. Furthermore, the distribution you are trying to match would have a theoretical frequency. Then, the Chi square is summed across all cells.

Use the data values structured into cells and explicitly requires a calculated chi-square test statistic. The unknown distribution is tested, and likewise, the Degrees of Freedom vary according to the distribution.

GOF Distribution  | Degrees of Freedom

Normal | # cells – 3

Poisson | # cells – 2

Binomial | # cells – 2

Uniform | # cells – 1

Steps to perform Chi Square goodness of fit

Step1:

Firstly, define the null hypothesis and alternative hypothesis

• Null hypothesis (H₀): There is no difference between the observed value and the expected value
• Alternative hypothesis (H₁): There  is a significant difference between the observed value and the expected value

Step 2:

Secondly, specify the level of significance

Step 3:

Thirdly, compute the χ2 statistic

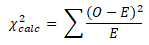
• O is the observed value
• E is the expected value

Step 4:

Fourthly, calculate the degree of freedom:

The degrees of freedom in chi square test depend on the sample distribution

Step 5:

Then, find the critical value, based on degrees of freedom

Step 6:

Finally, draw the statistical conclusion:

If the test statistic value is greater than the critical value, reject the null hypothesis, and hence we can conclude that there is a significant difference between the observed value and the expected value.

Chi Square goodness of fit test Example 1: Did the Distribution Change?

Ten years ago, US airlines categorized the priority customers (those who completed 10,000 miles traveled in a year) based specifically on age

Similarly, in 2020, 500 priority passengers are sampled, and below are the results

At a 95% confidence level, would you conclude that the population distribution of priority customers changed in the last 10 years?

• Null hypothesis (H₀): The sample data meet the expected distribution.
• Alternative hypothesis (H₁): The sample data does not meet the expected distribution.

Level of significance: α=0.05

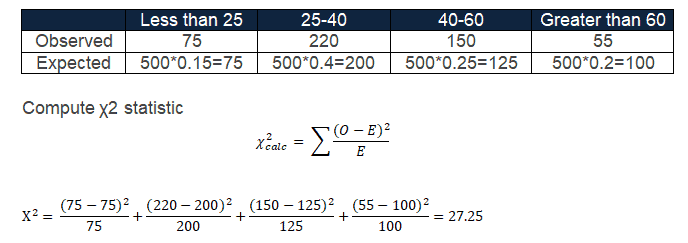
Degrees of freedom = number of categories (n)= 4

n-1 =3

Chi-square critical value for 3 degrees of freedom =7.815

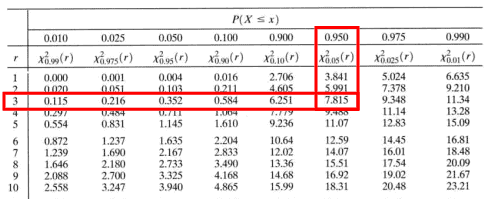
The test statistic value is greater than the critical value; hence, we can reject the null hypothesis.

So, we can conclude that the priority customers in 2020 are different than those expected based on the 2010 population.

Download Chi Square Goodness of Fit Exemplar

Chi Square Normality Test

Many statistical techniques (regression, ANOVA, t-tests, etc.) rely on the assumption that data is normally distributed. Hence, the Chi-square goodness of fit test is one of the good options to check whether the data follows a normal distribution.

Furthermore, the Chi-square goodness of fit test is an alternative to the Anderson-Darling test, Kolmogorov-Smirnov (K-S) test, and Shapiro-Wilk test to test the normality.

Similar to other statistical hypothesis tests, the Chi-square goodness of fit test also needs to compute the test statistics and find the critical value for a given degree of freedom and confidence level. If the Chi-Square value is greater than the critical value, reject the null hypothesis.

How to conduct Chi Square goodness fit normality test

• Determine the null hypothesis, i.e. data is sampled from a normal distribution and alternative hypothesis.
• Compute the sample mean as well as the standard deviation.
• Then, define the confidence level
• Bin the data: Determine non-overlapping bins, and then count values in each bin
• Furthermore, find the cumulative probability for each category endpoint.
• After that, compute the probability that a randomly selected value would go in each category
• Find expected observations for each bin, which is the product of the probability of observation would fall in the bin compared to the sample size (n)
• Likewise, compute the chi-square statistic. χ2 = Σ [ ( Observed frequency – Exp frequency) 2 / Exp frequency]
• Find the degrees of freedom based specifically on the number of categories or bins. The degrees of freedom for the Chi-square goodness of fit test is always the number of categories-1-2(two estimated parameters, mean and standard deviation) = k-3 (note: valid if mean and standard deviation are not given)
• Find the critical value, based on degrees of freedom.
• Finally, draw the statistical conclusion: If the test statistic value is greater than the critical value, reject the null hypothesis.

Chi Square normality test example

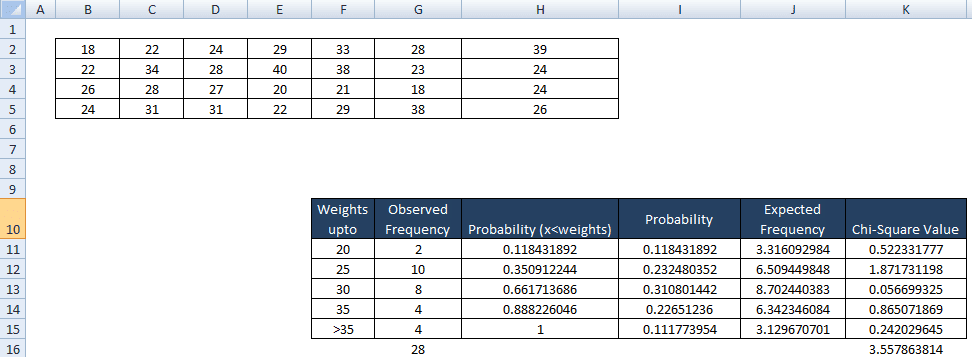
Example: 28 students’ weights (in kgs) are collected in ABC school. Test whether the data is normally distributed given that the confidence level is 95%.

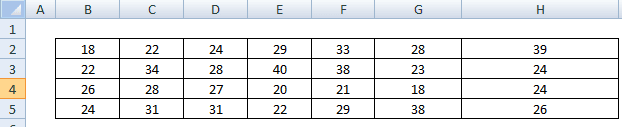
• H₀: Students’ weights in an ABC school follow a normal distribution
• H₁: Students’ weights in an ABC school do not follow a normal distribution

Firstly, compute the sample mean and standard deviation.

• Select all the data and enter” =Average(B2:H5)” for mean and “ Stdev(B2:H5)” for standard deviation
• Confidence level = 95%

Secondly, bin or categories the data and count the values

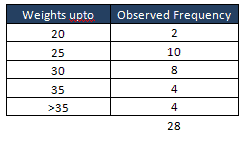
Thirdly, find the cumulative probability for each category endpoint.

• In cell H11 type NORMDIST (20, L2, L4, TRUE),
• Similarly H12 =  NORMDIST (25, L2, L4, TRUE),
• H13 =  NORMDIST (30, L2, L4, TRUE),
• H14=  NORMDIST (35, L2, L4, TRUE),
• H15 =  NORMDIST (∞, L2, L4, TRUE),

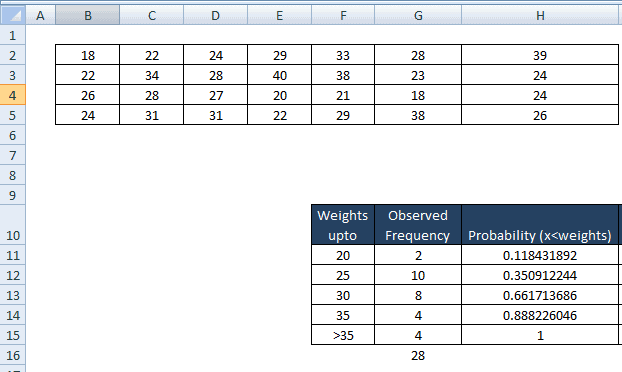
Fourthly, compute the probability that a randomly selected value would go in each category

• For I 11 cell, ie less than 20 copy the same value ie 0.118431892
• In cell I 12, i.e. values between 25 to 20= H12-H11 = 0.350912244-0.118431892 = 0.232480352
• Similarly for I13 = H13-H12=0.310801442
• I14 = H14-H13 = 0.226512236
• I15 = H15-H14 = 0.111773954

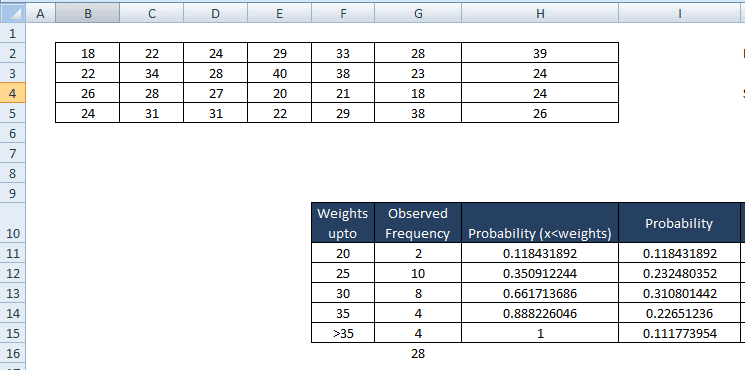
Then, find expected observations in each bin, which is the product of the probability of observation would fall in the bin to the sample size (n) =28

• J11 = I11*$G$16 = 3.316092984
• Similarly, J12=I12*$G$16=6.509449848
• J13=I13*$G$16=8.702440383
• J14=I14*$G$16=6.342346084
• J15= I15*$G$16=3.129670701

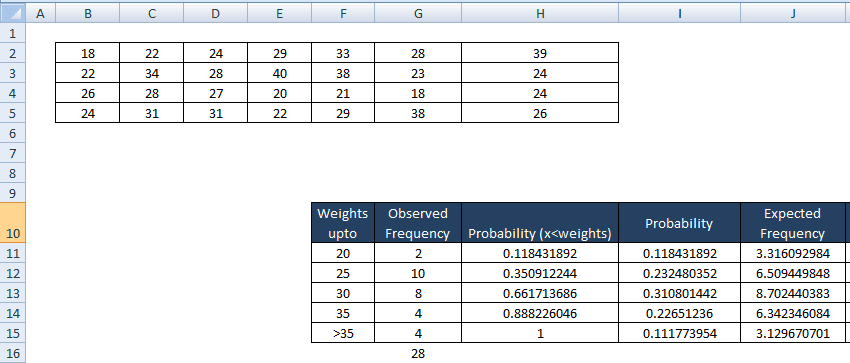
Finally, find the chi-square statistic. χ² = Σ [ ( Observed frequency – Exp frequency) ² / Exp frequency]

• K11 = (G11-J11)²/J11 = 0.522331777
• Similarly, K12 =  (G12 – J12)² / J12 = 1.871731198
• K13=(G13-J13)²/J13=0.056699325
• K14=(G14-J14)²/J14 = 0.865071869
• K15=(G15-J15)²/J15 = 0.242029645
• Then, find the sum of Chi-Square values = K16= sum(K11:K15) =3.55786

• Following that logic, the Degrees of freedom = No of categories -3 =5-3 =2
• Consequently, the Critical value =5.991

Conclusion: The chi-square value of 3.557 is less than the critical value of 5.991. In hypothesis testing, a critical value is a point on the test distribution that is compared to the test statistic to determine whether to reject the null hypothesis. if the chi-square calculated was smaller than the critical value, then the data did fit the model, therefore, failed to reject the null hypothesis. So, students’ weights in ABC school follow a normal distribution.

Download Chi Square Test of Normality Exemplar

Chi Square Normality Testing

• https://www.statisticshowto.datasciencecentral.com/chi-square-test-normality/