Linear regression is a statistical technique to estimate the mathematical relationship between a dependent variable (usually denoted as Y) and an independent variable (usually denoted as X). In other words, predict the change in the dependent variable according to the change in the independent variable.
- Dependent variable or Criterion variable – is the variable for which we wish to make a predictions
- Independent variable or Predictor variable – The variable used to explain the dependent variable
When to Use Linear Regression
In simple linear regression, there is only one independent variable used to predict a single dependent variable. Whereas, in multiple linear regression more than one independent variables used to predict a single dependent variable. In fact, the basic difference between simple and multiple regression is in terms of explanatory variables.
For example compare the crop yield rate against the rain fall rate in a season.
Notes about Linear Regression
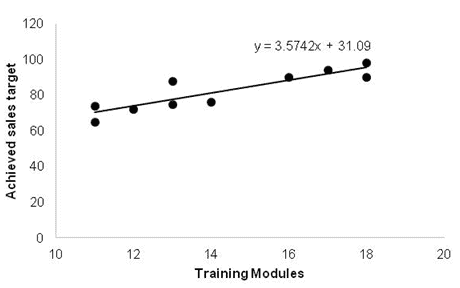
The first step of linear regression is to test the linearity assumption, this can be performed by plot the values in a graph known as scatter plot, to observe the relationship between dependent and independent variable, because if the data is exponentially scattered then there is no meaning to create the regression equation.
Draw the line which covers the majority of the points, further this line considered as the “best fit” line
The mathematical equation of the line is y=a+bx+ε
Where
- b – Slope of the line
- a – y intercept when x=0
- Random error (ε-Epsilon) – The difference between an observed value of y and the mean value of y for a given value of x.
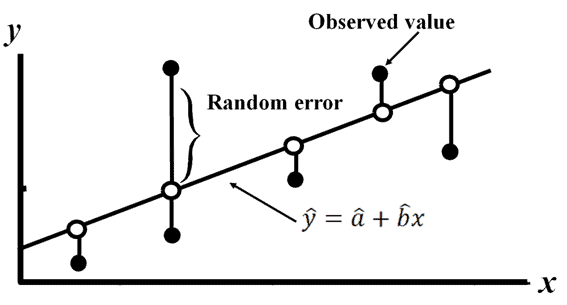
Assumption of Linear regression
- Linear relationship between dependent and independent variable
- All variables of regression to be multivariate normal
- Particularly there is no or little multicollinearity in the data
- Response variable is continuous and also residuals are almost same throughout the regression line
The method of Least Squares
The method of least squares is a standard approach in regression analysis to determine the best fit line for a given data, It basically provides a visual relationship between the given data points.
In general, the dependent variables are demonstrated on y-axis, while the independent variables are demonstrated on x-axis. The least square method determines the position of a straight line or also called trend line and the equation of the line. This straight line is also known as best fit line.
The least square method means that the overall solution minimizes the sum of squares of the errors made in the results of every single equation. For instance, Least Squares Equation can be used to find the values of the coefficients a and b
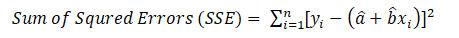
The least square estimator of a and b are compute as follows:
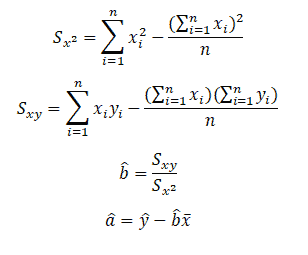
Compute â and b̂ values and then substitute these values into the equation of a line to obtain the least squares prediction equation or regression line
Linear Regression example in DMAIC
Example: Linear Regression is specifically uses in Analyze phase of DMAIC to estimate the mathematical relationship between a dependent variable and an independent variable.
A passenger vehicle manufacturer reviewing the 10 salespersons training records. In fact, their main aim is to compare the salespersons achieved target (in %) with the number of sales module training’ completed.
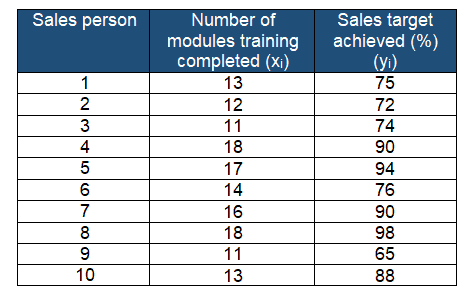
Compute the least square prediction equation or regression line
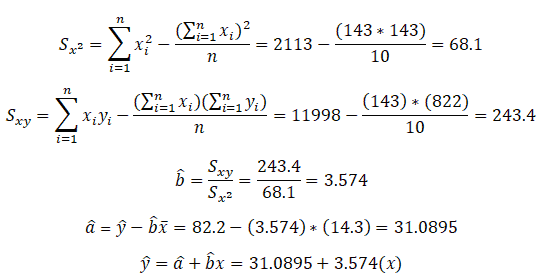
Furthermore, predict y for a given value of x by substitution into the prediction equation. For example, If a salesperson completes 15 training modules, then the predicted achieved target sales would be:
ŷ = 31.09+3.5742(15)= 84.7019=84.7%
Estimate the variability of random errors
Referring the mathematical equation of the line is y=a+bx+ε and also the least square line is
A random error (Є) affects the error of prediction. Hence the variability of the random errors (σε2) is the key parameter while predicting by the least squares line.
Estimate variability of the random error σε2
Example: From the above data, compute the variability of the random errors
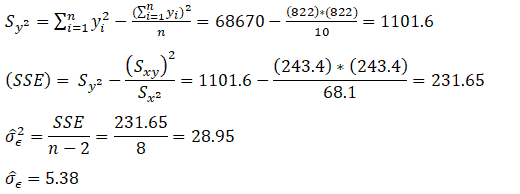
From the above calculation σ̂Є is 5.38. Thus, most of the points will fall within ±1.96 σ̂Є i.e 10.54 of the line, hence approx 95% of the values should be in this region. Moreover from the above graph, it is clearly evident that all the values are within ±10.54 of the line.
Test of slope coefficient
The existence of a significant relationship between dependent and independent variable can be tested by whether b is equal to 0. If b is not equal to 0 there is a linear relationship. The null and alternative hypotheses are
- The null hypothesis H0 : b=0
- The alternative hypothesis H1: b≠0
Degrees of freedom = n-2
Example: From the above data determine if the slope results are significant at a 95% confidence level
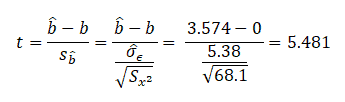
Determine the critical values of t for 8 degrees of freedom at 95% confidence level
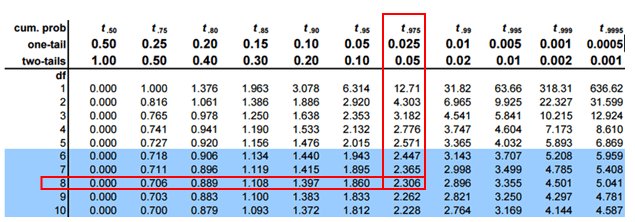
t0.025, 8 = -2.306 and 2.306
The calculated t value is 5.481, which is not in between -2.306 and 2.306, we can reject the null hypothesis if t value is greater than 2.306 or less than -2.306
In this case, we can reject the null hypothesis and concluded that b≠0 and there is a linear relationship between dependent and independent variable
Confidence interval estimate for the slop b
The confidence interval estimate for the slope b is
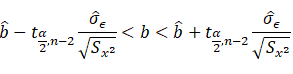
Example: from the above data, compute the confidence interval around the slope of the line
2.0707<b<5.07
Correlation Coefficient
The linear correlation coefficient r measures the strength of the linear relationship between the paired x and y values in a sample.
Pearson’s Correlation Coefficient
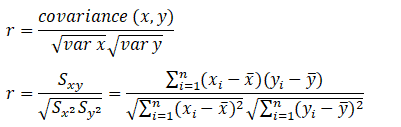
Example: from the above data, find the correlation coefficient
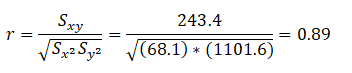
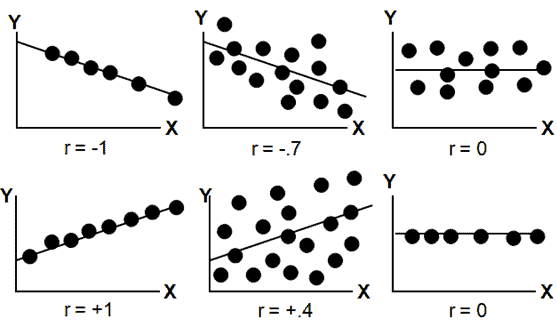
Note that -1≤ r ≤ +1
- The line slopes upward to the right when r indicates positive value
- The line slopes downward to the right when r indicates negative value
- A value closer to 1, indicates the stronger positive linear relationship
- A value closer to -1, indicates the stronger negative linear relationship
- When r=0 implies no linear correlation
How is correlation analysis used to compare bivariate data?
Measure of central tendency, variance, or spread summarizes a single variable by providing important information about its distribution. Often, more than one variable is collected in a study or experiment. When two variables are measured on a single experiment unit, the resulting data are called bivariate data. Ex job satisfaction stratified by income.
In most instances, in bivariate data, it determines that one variable influences the other variable. The quantities from these two variables often represented using scatter plots to explore the relation between two variables.
Depends on the type of data, Bivariate data can be described with graphs and numerical measures. If one or both variables are qualitative, then use a pie chart or bar chart to see the relation between variables. For example, compare the relationship between opinion and gender. If the two variables are quantitative, use the scatter plot. The Correlation Coefficient is often used in comparing bivariate data.
Example: Correlation between the amount of time spent in Casino (independent variable) and the amount ($) lost (dependent variable).
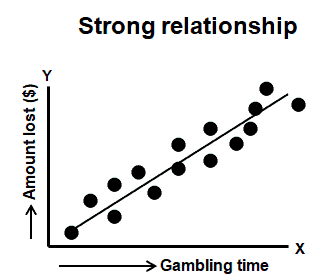
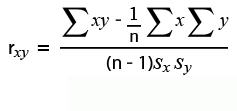
The correlation coefficient varies between -1 and +1. Values approaching -1 or +1 indicate strong correlation (negative or positive) and values close to 0 indicate little or no correlation between x and y.
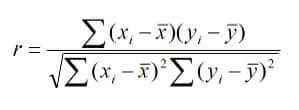
Correlation does not mean causation.
A positive correlation can be either good news or bad news
A negative correlation is not necessarily bad news. It merely means that as the independent variable goes more negative, the dependent variable goes negative as well.
r = 0; does not indicate the absence of a relationship, a curvilinear pattern may exist; r=-0.76 has the same predictive power as r = +0.76
Correlation Coefficient Videos
Coefficient of determination (R2)
The coefficient of determination is the proportion of the explained variation divided by the total variation, when a linear regression is performed.
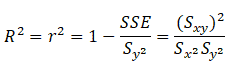
r2 lines in the interval of 0≤ r2 ≤1.
Example: from the above data, compute the coefficient of determination
We can say that 79% of the variation in sales target achieved can be explained by variation in number of training modules completed.
Linear Regression Related Topics
Residual Analysis: “Because a linear regression model is not always appropriate for the data, you should assess the appropriateness of the model by defining residuals and examining residual plots.”
Comments (7)
link does not work
Ted the link doesn’t work.Could you kindly provide a valide one?Thank you!
Hi all, Updated with a few links and a few videos. Let me know how this works for you!
Best, Ted.
All your contributions are very useful for professionals and non-professionals. I appreciate your availability to share these types of great and valuable info And you did it very well! Can’t wait to read more… You nailed it……..
Thanks for the kind words, Lyla!
Ted,Can you explain how the 1.96 and10.54 is derived?
From the above calculation σ̂Є is 5.38. Thus, most of the points will fall within ±1.96 σ̂Є i.e 10.54 of the line, hence approx 95% of the values should be in this region. Moreover from the above graph, it is clearly evident that all the values are within ±10.54 of the line.
Anshika,
A random error (Є) affects the error of prediction. Hence the variability of the random errors (σε2) is the key parameter while predicting by the least squares line.
Random errors in experimental measurements are caused by unknown and unpredictable changes in the experiment. Random errors often have a Gaussian normal distribution.
For the standard normal distribution, P(-1.96 < Z < 1.96) = 0.95, i.e., there is a 95% probability that a standard normal variable, Z, will fall between -1.96 and 1.96. (refer Z table)
From the calculation variability of random error is 5.38. 1.96 *5.38 = 10.54. 95% of values should be in this region, but If you observe above graph (in the example) all the points fall with in ± 10.54 of the LS line.
Hope this clarifies!
Thanks