The one and two sample proportion hypothesis tests involving one factor with one and two samples, these tests may assumes a binomial distribution. If more than two samples exist then use Chi-Square test.
One Sample Z Proportion Hypothesis Test
The One Sample Proportion Test is used to estimate the proportion of a population. It compares the proportion to a target or reference value and also calculates a range of values that is likely to include the population proportion. This is also called hypothesis of inequality.
Use normal approximation or binomial enumeration based on the sample size. If the sample size is large, then normal approximation will give more accurate results. If the sample sizes is less then binomial enumeration gives much more accurate results.
Assumptions of the one sample Z Proportion test
- The data are simple random values from the population
- Population follows a binomial distribution
- When both mean (np) and variance( n(1-p)) values are greater than 10, the binomial distribution can be approximated by the normal distribution
Hypothesis of one sample Z proportion test
- Null hypothesis: population proportion is equal to hypothesized proportion
- Alternative hypothesis: population proportion is not equal to hypothesized proportion (two -tailed)
- Population proportion is greater than hypothesized proportion (one -tailed)
- Population proportion is less than hypothesized proportion (one -tailed)
Test statistic for one sample Z proportions test
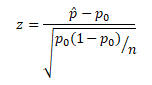
Where
- z is test statistic
- p̂is observed proportion
- P0 is hypothesized probability
- n is sample size
Procedure to execute One Sample Z Proportion Hypothesis Test
- State the null hypothesis and alternative hypothesis
- State alpha, in other words determine the significance level
- Compute the test statistic
- Determine the critical value (from critical value table)
- Define the rejection criteria
- Finally, interpret the result. If the test statistic falls in critical region, reject the null hypothesis
Example of One Sample Z Proportion Test
A researcher claims that Republican Party will win in next Senate elections especially in Florida State. A statistical data reported that 23% voted for Republican Party in last election. To test the claim a researcher surveyed 80 people and found 22 said they voted for Republican Party in last election. Is there enough evidence at α=0.05 to support this claim?
- P0=0.23
- n=80
- p̂=22/80=0.275
Define Null and Alternative hypothesis
- Null Hypothesis: p= 0.23
- Alternative Hypothesis: p≠0.23
State Alpha
- α=0.05
State decision rule
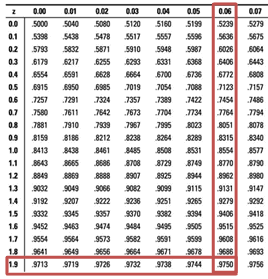
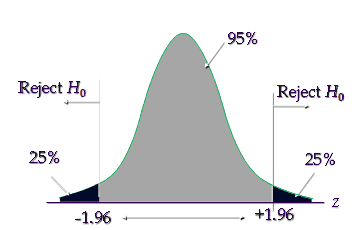
Critical value is ±1.96, hence reject the null hypothesis if the calculated value is less than -1.96 or greater than +1.96
Calculate test statistic
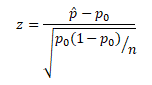
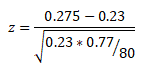
=0.045/0.047= 0.957
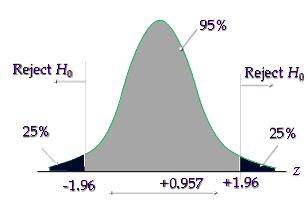
Since calculated value is in between -1.96 and 1.96 and it is not in critical region, hence failed to reject the null hypothesis.
Six Sigma Black Belt Certification One Sample Proportion Z Test Questions:
Question: Which of the following statement is true, the right tailed test of a single sample proportion test statistic value is +1.12 and the critical value from the table is +2.89.
(A) Reject the null hypothesis
(B) Failed to reject the null hypothesis
(C) Accept the null alternative hypothesis
(D) None of the above
Answer:
Unlock Additional Members-only Content!
To unlock additional content, please upgrade now to a full membership.Upgrade to a Full Membership
If you are a member, you can log in here.
Comments (2)
Good Day Ted,
When I solve this two sample test of proportions using the formula below from IASSC Reference Document, I get 2.26. Can you please advise if there’s a step I’m missing; or could this just be a difference resulting from rounding throughout solving?
P1-P2/ square root of P1(1 – P1)/n1 + P2(1- P2)/n2
Hi Lemarcus,
A few things:
1) I’ve moved the 2 Sample text and example to it’s own page here.
2) There are (2) versions of the 2 Sample Proportions test; a pooled version and the unpooled version. The IASSC equation sheet makes use of the unpooled equation while the ASQ, Villanova, and most other certifying bodies make use of the pooled version. The question you’re asking about is using the pooled version, hence why the equations are different.
I’ve added a bit more on the difference between pooled and unpooled here.
I’ll also update the article to have a walkthrough for both pooled and unpooled.
Best, Ted.