Analysis of Variance (ANOVA) is a parametric statistical technique used to compare data sets. This technique was invented by R.A. Fisher; hence, it is also referred to as Fisher’s ANOVA. It is similar to techniques such as t-test and z-test to compare means and also the relative variance between them.

Similarly, a t-test can be used to compare two sample means. What if we want to compare more than two means? Analysis of variance (ANOVA) is best applied where more than 2 populations or samples are meant to be compared.

It is used to test the statistical significance of the relationship between a dependent variable (“Y”) and single or multiple independent variables (“X’s”).

Types of ANOVA

• One-way
  • Measures single factor from multiple sources
  • Uses only one technician / one measurer
• Two-way (without replicates)
  • Measures 2 factors
  • Uses only one technician (unless technicians are one of the factors)
• Two-way (with replications)
  • Measures 2 factors but has multiple repetitions of each combination.
  • Uses only one technician (unless the technicians are one of the factors)

ANOVA Sum of Squares Correction Factor

• Grand total of all runs (G) = ΣX
• N= Total number of runs
• Correction factor (CF)= (ΣX)² /N = (G)² /N

Terms used in ANOVA

• Degrees of Freedom (df): The number of independent conclusions that can be drawn from the data. 
• SS_Factor: It measures the variation of each group’s mean to the overall mean across all groups. 
• SS_Error: It measures the variation of each observation within each factor level to the mean of the level. 
• Main effect: A main effect is an effect where the performance of one variable is considered in isolation by neglecting other variables in the study.
• Interaction: An interaction effect occurs where the effect of one variable is different across levels of one or more other variables.
• Mean Square Error (MSE): The mean square of the error (MSE) is divided by the sum of squares of the residual error by the degrees of freedom.
• F-test Statistic: The null hypothesis that the category means are equal in the population is tested by F Statistic based on the ratio of mean square related to X and mean square related to the error.
• P-value: It is the smallest level of significance that would lead to rejection of the null hypothesis (Ho). If α = 0.05 and the p-value ≤ 0.05, then reject the null hypothesis. Similarly if the p-value > 0.05, then fail to reject the null hypothesis.

https://youtu.be/x6F9uvaviEc

Analysis of Variance (ANOVA) has three types:

• One-way analysis
• Two-way analysis
• K-way analysis: K-Way ANOVA can be two-way ANOVA or three-way ANOVA, or multiple ANOVA

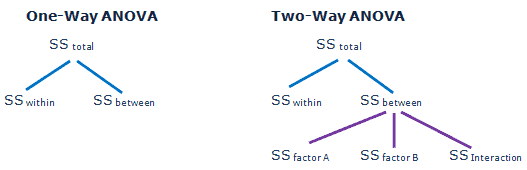
One way ANOVA

One-way ANOVA (one-way analysis of variance) is a statistical method to compare the means of two or more populations.

Assumptions of One-way ANOVA

• The sample data drawn from k populations are unbiased and representative.
• The data of k populations are continuous.
• The data of k populations are normally distributed.
• The variation within each factor or factor treatment combination is the same; hence, it is also called homogeneity of variance.
• Finally, the variances of k populations are equal.

Steps for Computing one-way ANOVA:

• Establish the hypotheses. H₀: µ1= µ2= µ3 and H₁: At least one group means differs from the others.
• In ANOVA, the total variance is subdivided into two independent variances: the variance due to the treatment and the variance due to random error.

• SS_T = SS_b + SS_w 
• Calculate the ANOVA table with degrees of freedom (df), and calculate the group’s error and total sum of squares.

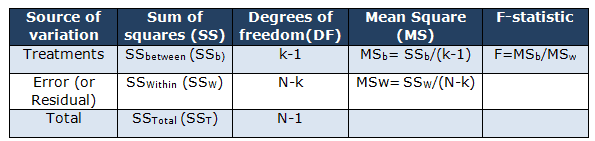
• SS_b= sum of squares between treatments
• SS_w= sum of squares due to error
• MS_b= mean square for treatments
• MS_W= mean square for error
• SS_T= total sum of squares
• T= number of treatment levels
• n= number of runs at a particular level
• N= total number of runs
• F= the calculation of the F Statistic with k-1, and N-k is the degrees of freedom.
• Determine the critical value. F critical value from the F distribution table.
• Finally, Draw the statistical conclusion. If Fcalc< Fcritical, fail to reject the null hypothesis, and if Fcalc > Fcritical, reject the null hypothesis.

Example of One-Way ANOVA

A car manufacturer planned to conduct tests to determine the performance of 3 different brands of 12V batteries, so he selected five batteries from each brand and discharged them under controlled conditions. Assuming the lifetime of batteries is normally distributed at a 95% confidence level. The hypothesis is that the three brands have no difference in lifetime.

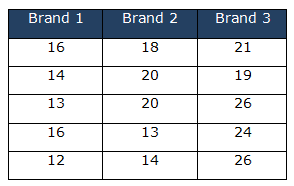
H₀: µ1= µ2= µ3

H₁: At least one of the brands mean life is different from the others.

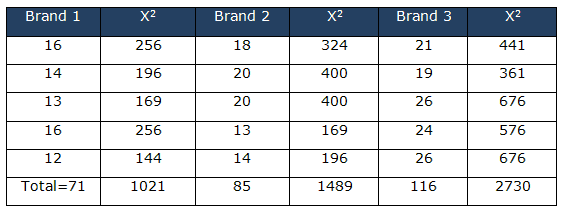
k = 3, n = 5, N = 15, T1 = 71, T2 = 85, and T3 = 116, and G = 272 ΣX²= 1021 + 1489 + 2730 = 5240

Correction factor (CF) = (ΣX)² /N = (G)² /N = (272)²/15

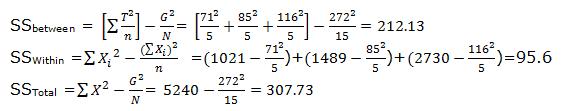
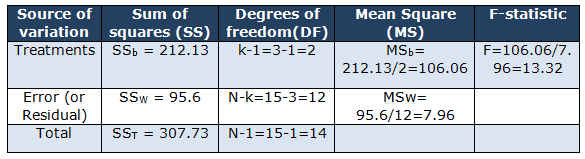
One-Way ANOVA Excel Download

A: analysis of variance (ANOVA). The other options don’t make any sense. In other words, An ANOVA is designed to compare three or more factors against each other- This is what happens in a designed experiment.

When you’re ready, there are a few ways I can help:

First, join 30,000+ other Six Sigma professionals by subscribing to my email newsletter. A short read every Monday to start your work week off correctly. Always free.

—

If you’re looking to pass your Six Sigma Green Belt or Black Belt exams, I’d recommend starting with my affordable study guide:

1)→ 🟢Pass Your Six Sigma Green Belt​​

2)→ ⚫Pass Your Six Sigma Black Belt ​​​

You’ve spent so much effort learning Lean Six Sigma. Why leave passing your certification exam up to chance? This comprehensive study guide offers 1,000+ exam-like questions for Green Belts (2,000+ for Black Belts) with full answer walkthroughs, access to instructors, detailed study material, and more.

​ Thousands have used this system to prepare. Join them here.