Sign Test

The 1 Sample Sign Non Parametric Hypothesis test was invented by Dr. Arbuthnot a Scottish physician in the year 1710. The Sign test is used to test the null hypothesis that the median of a distribution is equal to some hypothesized value k. The test is based on the direction or the data are recorded as plus and minus signs rather than numerical magnitude, hence it is called the Sign test.

Use sign test for the following:

• To determine the preference for one product over the other
• Conduct a test for the median of a single population (one sample sign test)
• To perform a test for the median of paired difference using the data from two dependent samples.

One Sample Sign Test

The One-sample Sign Test simply determines a significance test of a hypothesized median value for a single data set. The 1 sample sign test is a Non Parametric Hypothesis test used to determine whether a statistically significant difference exists between the median of a non-normally distributed continuous data set and a standard. This test basically concerns the median of a continuous population.

The 1 sample sign test is to compare the total number of observations less than (-ve) or greater than (+) the hypothesized value. The 1 sample sign test is similar to the One-sample Wilcoxon Signed-rank test but less powerful than the Wilcoxon signed test.

The One-sample Sign Test is a non parametric version of one sample t-test. Similar to one sample t-test, the sign test for a population median can be a one-tailed (right or left-tailed) or two-tailed distribution based on the hypothesis.

• Left tailed test- H₀:median≥ Hypothesized value k; H₁: median <k
• Right tailed test- H₀:median≤ Hypothesized value k; H₁: median >k
• Two-tailed test- H₀: median= Hypothesized value k; H₁: median ≠k

Assumptions of the one sample sign test

• Data is non-normally distributed.
• A random sample of independent measurements for a population with an unknown median
• The variable of interest is continuous
• 1 sample test handles a non-symmetric data set, which means skewed either to the right or the left.

Procedure to execute One Sample Sign Non Parametric Hypothesis Test

• State the claim of the test and determine the null hypothesis and alternative hypothesis
• Determine the level of significance
• Assign positive and negative signs to the sample data, and determine the sample size (n)- n is the sum of positive and negative signs
• Find critical value
• Compute the test statistic-
  • If n≤ 25 (approx), use y. Where y is the smaller number of positive and negative signs
  • For a larger sample size, if n > 25, use

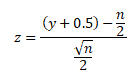
• Make a decision, the null hypothesis will be rejected if the test statistic is less than or equal to the critical value
• Interpret the decision in the context of the original claim.

Example of One Sample Sign Test

A Bank of America West Palm Beach, FL branch manager shows that the median number of savings account customers per day is 64. A clerk from the same branch claims that it was more than 64. The clerk found the number of savings accounts customers per day data for 10 random days. Can we reject the branch manager’s claim at a 0.05 significance level?

• Null Hypothesis H₀: Savings account customer median = 64;
• Alternative Hypothesis H₁: Savings account customer median >64

Assign observations less than 64 with a – sign and observations above 64 with a + sign

Total number of + values =8

Total number of – values =2

Test statistic is a minimum of (8,2) =2

Look at the Binomial table (10, 0.5)

• Note: 10- is the number of trails
• 0.5 – 50% chance more than the median value and 50% change less than the median value

At 0.05 significance level

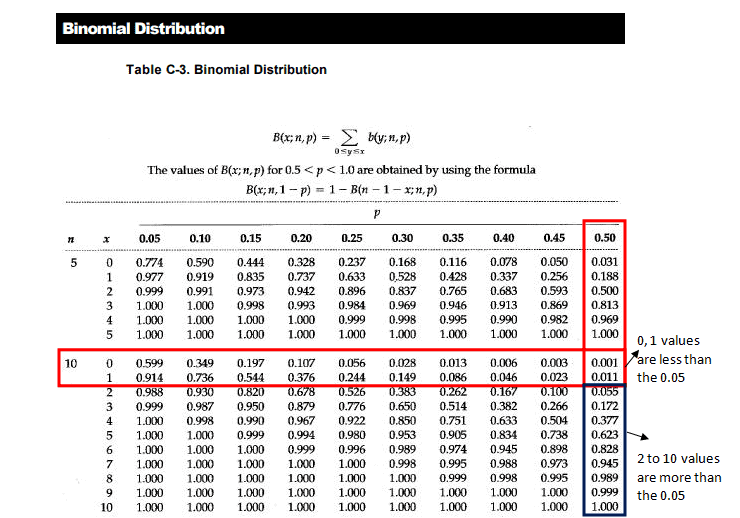
The probability for x=2 is 0.055, which is greater than 0.05. Since test statistic 2 is in the acceptance region ( H0), hence failed to reject the null hypothesis. So, there is no significant evidence that the number of savings account customers per day is more than 64.

Six Sigma Black Belt Certification 1 Sample Sign Non Parametric Hypothesis Test Questions:

Answer A:  The sign test uses the binomial distribution to determine whether a statistically significant difference exists between the median of a non-normally distributed continuous data set and a standard.