Single Sample Test Of a Given Proportion

Single sample test of a given proportion is used to estimate the proportion of the population. For example, to estimate the proportion of Spanish-speaking students in a school is lower than the state proportion. Basically, it is used to compare the proportion to a target or reference value.

Furthermore, the proportion test is to determine the percentage of individuals who have a particular characteristic. It also calculates a range that is likely to include the population proportion. Hence, proportion involves a binomial distribution.

Single sample test of a given proportion Formula

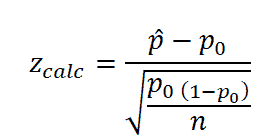
Where

• Z is test statistic
• p̂ is the sample or observed proportion
• P₀ hypothesized proportion
• n sample size

When to use

We use the Single sample test of a given proportion when both the independent (X) and dependent variables are discrete. Hence it follows a binomial distribution.

Assumptions of Single sample test of a given proportion test

• Population follows a binomial distribution.
• Sample is unbiased and representative
• Both main and variance np₀, n(1- p₀) for binomial distribution are both ≥5, then the sampling distribution can be approximated by the normal distribution.

Hypothesis of Single sample test of a given proportion

• Null hypothesis H₀: population proportion is equal to hypothesized proportion, in other words, p=p₀
• Alternative hypothesis H₁: population proportion is not equal to hypothesized proportion p≠p₀ (Two-tailed)
• H₁: Population proportion is less than hypothesized proportion p<p₀ (One-tailed)
• H₁: Population proportion is greater than hypothesized proportion p>p₀ (One-tailed)

How to calculate Single sample test of a given proportion

• First, estimate the proportion p, as  p̂ =x/n
  • Where x is the sample who have same characteristic, n is the sample size
• Select appropriate statistic- one-tailed or two-tailed?
• State the null hypothesis and alternative hypothesis
• State alpha, in other words determine the significance level
• Define the rejection criteria
• Check the assumption, both np₀, and n(1- p₀)≥5
• Compute the test statistic,

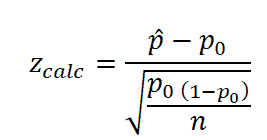
• Determine z critical value
• Finally, interpret the result. If the test statistic falls in critical region, then reject the null hypothesis.

Example of Single sample test of a given proportion

Right-Tailed

Example: A property leasing office is conducting a vaccination drive, and they are encouraging more women to participate in the event. While a sample of 4300 vaccination reports, it is indicated that 2200 are women. Property manager is confident that at least 49 percent of women participated in the drive. At α=0.05, were their vaccination drive efforts successful?

• P₀=0.49
• x=2200
• n=4300
• p̂=x/n=2200/4300=0.512

Define Null and Alternative hypothesis

• Null Hypothesis: population proportion is equal to hypothesized proportion p= 0.49
• Alternative Hypothesis: population proportion is greater than hypothesized proportion p>0.49

State Alpha

• α=0.05

Both np₀, and n(1- p₀)≥5

Calculate test statistic

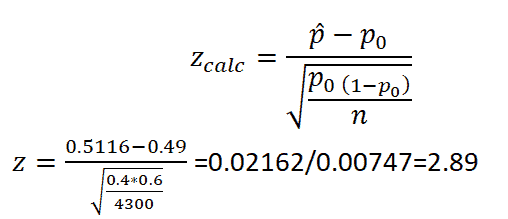
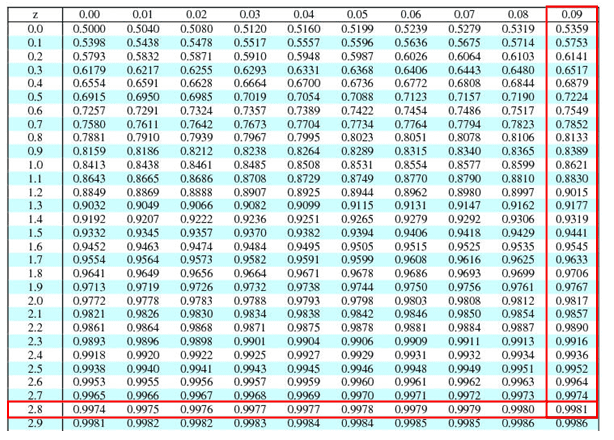
Since, we are looking for longer, P(Z>2.89) = 1- P(Z<2.89)= 1-0.9981 = 0.0019

Since p value (0.0019) is less than the alpha value (0.05), we have enough evidence to reject the null hypothesis which makes our test significant. Therefore vaccination drive is successful

Right Tailed Single Proportion template download

Important Videos