Basic Six Sigma Probability terms like independence, mutually exclusive, compound events, and more are necessary for statistical analysis.
The probability of an event E indicates how likely that event is to occur. Probability is the ratio of the number of favorable outcomes to the total number of possible outcomes. Probabilities are usually shown in fractions or decimals. The probability always lies between 0 and 1.
The sum of the probabilities of all possible events in a sample space S =1.
An event is one or more outcomes of an experiment.
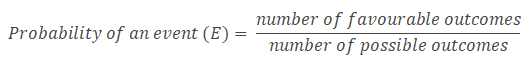
Example: The probability of getting 4 by throwing a single die is:

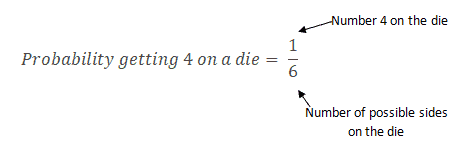
Similarly, what is the probability of observing 1,2,3,4,5, or 6 on the toss of a single die?
Probability of getting 1,2,3,4,5 or 6 = 1/6+1/6+1/6+1/6+1/6+1/6 = 1
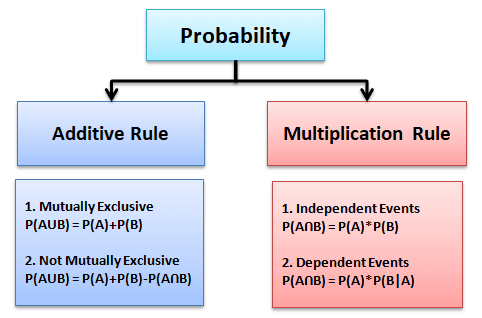
There are two basic rules in Probability: Additive rule and Multiplication rule:
Basic Six Sigma Probability Videos
Additive Law
What is the Additive Law?
The additive law of probability is also known as the addition rule. Additive law is the probability of the union of two events. There are two scenarios in additive law:
- When events are not mutually exclusive
- When events are mutually exclusive
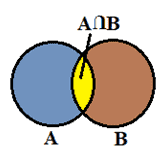
Two events are not mutually exclusive:
When two events A and B are not mutually exclusive, the probability that A and B will occur is the sum of the two events’ probabilities, and subtracting both probabilities of A and B will occur (intersection), the formula can summarize the same:
P (A U B) = P(A) + P(B) – P(A Ո B)
Two events are mutually exclusive:
When two events A and B are mutually exclusive, the probability of A and B will occur is the sum of the two events’ probabilities. The formula can summarize the same:
P (A U B) = P(A) + P(B)
When Would You Use the Additive Law in a Six Sigma Project?
Additive law is essential in probability. Additive law tells us a way to calculate the probability of an event “A” or the probability of “B.” The use of additive law depends on whether event A and event B are mutually exclusive.
A Six Sigma Example of the Additive Law
Two events are not mutually exclusive.
Example 1: Two cars, each with a 60% chance of starting. What are the chances that at least one of them starts?

P = .6 + .6 – (.6*.6) = 1.2 – .36 = .84
Two events are mutually exclusive.
Example 2: What is the probability of drawing an Ace OR a King from a 52-card deck?
P (A U B) = P(A) + P(B)

P = 4/52 + 4/52 = 8/52 = 2/13
Multiplication Law
What is the Multiplication Law?
The multiplication law is a method to find the probability of events occurring simultaneously. There are two scenarios in multiplication law:
- When events are independent
- When events are dependent
Two events are Independent:
When two independent events A and B are occurring from the same sample space, the probability of two events happening at the same time is equal to that of A occurring times the probability of B occurring. The formula can summarize the same:
P (A Ո B) = P(A) * P(B)
Two events are dependent:
When two dependent events A and B, are occurring from the same sample space, then the probability of two events happening at the same time is equal to the probability of A occurring times the probability of B occurring, given that A has already occurred. This is a conditional probability. The formula can summarize the same:
P (A Ո B) = P(A) * P(B|A)
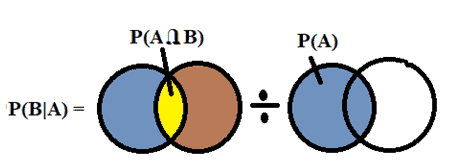
When Would You Use the Multiplication Law in a Six Sigma Project?
When the events have to occur together, then make use multiplication law of probability in Six Sigma projects.
A Six Sigma Example of the Multiplication Law
Two events are independent.
Example 1: Two cars, Car A has a 60% chance of starting, and Car B has a 70% of starting. What is the probability of both cars starting simultaneously?

P (A Ո B) = P(A) * P(B)
P = 0.6 * 0.7 = = 0.42
Two events are dependent.
Example 2: Suppose A is the first event drawing King from a 52-card deck, and B is the second event drawing the King card from the rest of the cards. Then the probability is:

P (A Ո B) = P(A) * P(B|A)
P (A Ո B) = 4/52 * 3/51 = 0.0045
Note: Here, the second denominator is only 51, as already one card has been drawn.
Mutually Exclusive Events
What are Mutually Exclusive Events?
Mutually exclusive events are things cannot both be true. In other words, they cannot occur at the same time.
When Would You Use Mutually Exclusivity in a Six Sigma Project?
Mutually exclusive events are used in Six Sigma projects. When one event occurs, it prevents the second from happening.
A Six Sigma Example of the Mutually Exclusive Probability
Example: When you flip a coin, what is the probability of getting both heads and tails simultaneously?

Probability of happening both had and tails same time:
P(head and tails) =0 or P(head Ո tails) =0
Example: What is the probability of rolling one 6-sided die and getting either a 3 or a 4?
P (A or B) = P(A) + P(B)
P (3 or 4) = P(3) + P(4) = 1/6 + 1/6 = 1/3 = 33%
Complementary probability
Complementary probability is a statistical concept that refers to the probability of an event not occurring. It is often denoted by the symbol “P(A’).” A ′ represents the complement of A. The complement (A′) includes all outcomes in the sample space that are not the outcomes of event A. In other words, it consists of all outcomes in which event A does not occur.
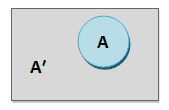
An event (A) and its complement (A′) are mutually exclusive, which means either event (A) or its complement (A′) will occur, not both at a time. Hence the complement rule is the sum of the probability of an event (A), and its complement (A′) is 1.
Probability of event occurring P(A) = Number of times the event happens / Total number of possible outcomes
Probability of event not occurring P(A′) = 1- (Number of times the event happens / Total number of possible outcomes)
P (A′) =1-P(A)
P (A) +P (A′) =1
For example, if the probability of rolling a 4 on a standard six-sided die is 1/6, then the complementary probability of not rolling a 4 is:
P(A’) = 1 – P(A) = 1 – 1/6 = 5/6
Therefore, the complementary probability of not rolling a 4 on a standard six-sided die is 5/6.
Example: When tossing a coin, if the event (A) is tails, then the complement (A′) is heads.
If you are throwing a die and the event (A) is even {2,4,6} then the complement(A′) is {1,3,5}.
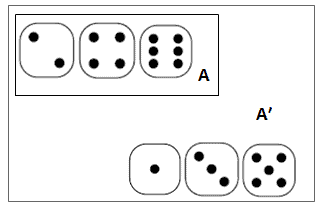
Complimentary probability is often used in statistical calculations and hypothesis testing, and it is a useful tool for understanding the relationship between different events and their probabilities.
Joint occurrence of events
The joint occurrence of events refers to the probability that two or more events will occur together. In other words, it is the probability that multiple events will happen simultaneously or in combination.
The joint probability of two events A and B can be denoted as P(A and B) and is calculated as the product of their individual probabilities.
P(A and B) = P(A) x P(B)
For example: Rolling a 4 on the die and flipping a coin, and getting tails. The probability of rolling on a die is 1/6, and the probability of flipping a coin and getting tails is 1/2. The joint probability of both events happening together is:
P(rolling a 4 and getting tails) = P(rolling a 4) x P(getting tails) = (1/6) x (1/2) = 1/12
Therefore, the joint probability of rolling a 4 and getting tails is 1/12.
Compound Events
What are Compound Events?
A compound event is when there is more than one possible outcome of an experiment. In other words, compound events are composed of two or more events. They consist of more than one point in the sample space.
When Would You Use Compound Events
Compound events are used when the outcome may have different probabilities, but they are all equally possible. Events that are chained together in a row.
A Six Sigma Example of Compound Events
Example: If two dice are tossed. What are the outcomes for the event that the sum of two dies is less than 5?
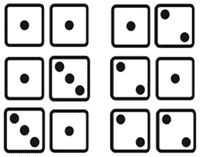
(1,1), (1,3), (3,1),(1,2), (2,1), and (2,2)
Independent Events
What Are Independent Events?
Events can be independent events when the outcome of one event does not influence another event’s outcome. In other words, each event is not affected by other events.
Whereas the dependent event is the probability of one event occurring that influences another event.
When Would You Use Independent Events in a Six Sigma Project?
Independent events are used in Six Sigma projects where one event does not connect with another event’s chance of occurring. The car mileage does not depend on the color of the car.
An Example of Independent Events
Example: What is the probability of rolling one 6-sided die thrice and getting a 2 on the first roll, 3 on the second roll, and a 4 on the third roll?

Since the roll of the second and third die can be anything–no matter what happens on the first roll–they are considered independent events.
P (A and B and C) = P(A) * P(B) * P(C)
P (2 and 3 and 4) = P(2) * P(3) * P(4) = 1/6 * 1/6 * 1/6 = 1/216
Sampling Without Replacement

Sampling Without Replacement is a probability question that is an example of using the Hypergeometric Distribution.
If the sample size was great compared to the population size, then we could use Binomial distribution to approximate.
Sampling Without Replacement Equation and Terms
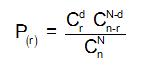
Remember that C(a / b) = a! / (b! * (a-b)!)
Population Size: N =
Sample Size: n =
Occurrences in sample: r = 0
Occurrences in population: d =
Sampling Without Replacement Example:
Five books are damaged out of a set of 15. What is the probability of selecting 3 undamaged books when you pull without replacing them?
First, compare the sample size to the population.
We see that the sample size (3) is small compared to the overall population size (15). Thus, we will use the hypergeometric distribution.
Next, we identify the terms:
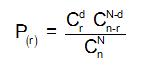
Population Size: N = 15
Sample Size: n = 3
Occurrences in sample: r = 0
Occurrences in population: d = 5
P = C(5/0) * C(10/3) / C(15/3)
C(a/b) = a! / (b! * (a-b)!)
P = 0.2637
Basic Six Sigma Probability Videos
When you’re ready, there are a few ways I can help:
First, join 30,000+ other Six Sigma professionals by subscribing to my email newsletter. A short read every Monday to start your work week off correctly. Always free.
—
If you’re looking to pass your Six Sigma Green Belt or Black Belt exams, I’d recommend starting with my affordable study guide:
1)→ 🟢Pass Your Six Sigma Green Belt
2)→ ⚫Pass Your Six Sigma Black Belt
You’ve spent so much effort learning Lean Six Sigma. Why leave passing your certification exam up to chance? This comprehensive study guide offers 1,000+ exam-like questions for Green Belts (2,000+ for Black Belts) with full answer walkthroughs, access to instructors, detailed study material, and more.


Comments (20)
YOU WERE TO ROLL A SIGLE DIE 10 TIMES,WHAT WOULD THE RESULTS OF EACH ROLL WOULD
BE
A. MUTUALLY EXCLUSIVE OF THE OTHER NINE ROLLS
B. PROPORTIONAL TO THE OTHER NINE ROLLS
C. DEPENDENT UPON THE OTHER NINE ROLLS
D. INDEPENDENT OF THE OTHER NINE ROLLS.
Thank you for the question, Kelvin. I’ve addressed this in the member section. Best, Ted.
On the given example below how would changing the desired outcome would affect the event type?
Example: 2 cars, each with a 60% chance of starting. What are the chances that at least one of them starts?
A) what are the chances of both start at the first try?
A2) what are the chances of both to start?
B) if one care has 60% chance and the other 30% chance. What are the chances that at least one of them starts?
B2) what are the chances of both start at the first try?
B3) what are the chances of both start?
Very helpful videos guys, thank you for taking the time of sharing the knowledge!
Carlos,
Each of those questions you list is a specific type of probability (ie mutually exclusive, additive, compound, etc).
Start by identifying what kind of event is going on.
Next, look at how you’re supposed to treat each event and substitute the values in.
Write back and show me what you’ve tried.
Hi Ted,
I’m trying to figure out how the author of the last youtube video re: “Basics of Probability- Binomial & Poisson calculated the Poisson Equation.
Hi Ted,
I’m trying to figure out how the author of the last video re: “Basics of Probability- Binomial & Poisson calculated the Poisson Equation.
The question was if 100 pages were randomly selected, what was the probability of “no typos”
If x=0 & lambda=1.5
P(0)= 1.50 o x e-1.5/0!
I am lost with how he got 0.2231? Might be simple algebra (but I think I’m missing something)?
Thank you
Hi Cheryl,
Thanks for the question. I don’t support the videos attached. They’re here as a convenience for people who need a refresher. But I will try to address this later on.
I can answer any questions about the content inside the course there.
Best, Ted.
Cheryl,
I found it helpful to pause the video at around 8:37 and jot down the formula with the numbers populated. Its a little tricky because you have two values that are actually just equal to 1. Both 1.5^0 and 0! are equal to 1 so all you really have to worry about is the e^-1.5 which gives you the 0.223
e^-1.5 is calculated by sing the negative exponent rule, which states b^-n = 1/b^n.
So, this makes e^-1.5 = 1/e^1.5.
1/e^1.5 = 1/4.4817 = 0.2231. Hope this helps!
What does K stand for in the probability calculation?
Which calculation, Sarah?
There’s a section above on Mutually Exclusive Events. It reads:
“Mutually exclusive events are things cannot both be true.Mutually exclusive events are things that cannot both be true. In other words, they cannot occur the same time.Mutually exclusive events are things cannot both be true.”
The same phrase is repeated 3 times in the same paragraph.
Thank you Tanner Zornes, Updated the verbiage
Thanks
Did you meant he below to be Two events are NOT independent based on your above mentioned two scenarios for the Multiplication Law:
Two events are Independent:
When two independent events A and B are occurring from the same sample space, then the probability of two events occurring at the same is equal to the probability of A occurs times the probability of B occurs. The formula can summarize the same:
P (A Ո B) = P(A) * P(B)
Scratch the above comment – the wording confused me
Hi Sahannon,
The first one is two events are independent. Updated the bullet points
Thanks
Example: What is the probability of rolling one 6 sided die thrice and getting a 2 on the first roll, 3 on the second roll and a 4 on the third roll? Here why have you multiplied the probabilities? Shouldn’t we add them? Because it is are rolled three times one after the other and not at the same time? So P(1) +P(2) + P(3)
Hi Fathima,
We multiply because the order of the results matter. We want to get a 2 on the first roll, then a 3 on the second, etc.
If we wanted the probability of getting a 2, 3, or a 4 on one roll we would add them.
Best, Ted.
Moved to member forum
An indoor board game consists of 25 tickets numbered 1 to 25. A player randomly draws one ticket. What is the probability that the ticket number is multiples of 4 or 6?
Correct answer: 9/25
Explanation: Total possible outcomes =25
Event of multiple of 4 and 6 getting tickets = {4,8,12,16,20,24,6,18,24} =9
Hence P(Event) = 9/25
–> this is incorrect as there are only 8 possible events. Your answer lists “24” twice
Hello Wiebke Zuch,
You are correct. We have to consider 24 only once as it is common for multiple of 4 and 6.
Hence P(Event ) is 8/25.
We updated the question pool. Thanks for your feedback.
Thanks