Basic Six Sigma Probability

Basic Six Sigma Probability terms like independence, mutually exclusive, compound events, and more are necessary for statistical analysis.

The probability of an event E indicates how likely that event is to occur. Probability is the ratio of the number of favorable outcomes to the total number of possible outcomes. Probabilities are usually shown in fractions or decimals. The probability always lies between 0 and 1.

The sum of the probabilities of all possible events in a sample space S =1.

An event is one or more outcomes of an experiment.

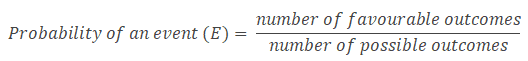
Example: The probability of getting 4 by throwing a single die is:

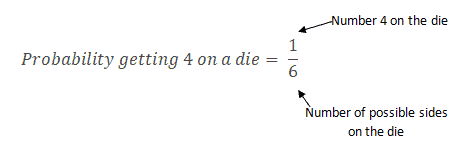
Similarly, what is the probability of observing 1,2,3,4,5, or 6 on the toss of a single die?

Probability of getting 1,2,3,4,5 or 6 = 1/6+1/6+1/6+1/6+1/6+1/6 = 1

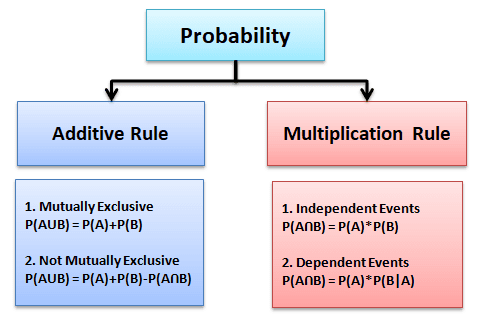
There are two basic rules in Probability: Additive rule and Multiplication rule:

Basic Six Sigma Probability Videos

Additive Law

What is the Additive Law?

The additive law of probability is also known as the addition rule. Additive law is the probability of the union of two events. There are two scenarios in additive law:

• When events are not mutually exclusive
• When events are mutually exclusive

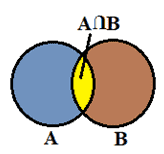
Two events are not mutually exclusive:

When two events A and B are not mutually exclusive, the probability that A and B will occur is the sum of the two events’ probabilities, and subtracting both probabilities of A and B will occur (intersection), the formula can summarize the same:

P (A U B) = P(A) + P(B) – P(A Ո B)

Two events are mutually exclusive:

When two events A and B are mutually exclusive, the probability of A and B will occur is the sum of the two events’ probabilities. The formula can summarize the same:

P (A U B) = P(A) + P(B)

When Would You Use the Additive Law in a Six Sigma Project?

Additive law is essential in probability. Additive law tells us a way to calculate the probability of an event “A” or the probability of “B.” The use of additive law depends on whether event A and event B are mutually exclusive.

A Six Sigma Example of the Additive Law

Two events are not mutually exclusive.

Example 1: Two cars, each with a 60% chance of starting. What are the chances that at least one of them starts?

P = .6 + .6 – (.6*.6) = 1.2 – .36 = .84

Two events are mutually exclusive.

Example 2:  What is the probability of drawing an Ace OR a King from a 52-card deck?

P (A U B) = P(A) + P(B)

P = 4/52 + 4/52 = 8/52 = 2/13

Multiplication Law

What is the Multiplication Law?

The multiplication law is a method to find the probability of events occurring simultaneously. There are two scenarios in multiplication law:

• When events are independent
• When events are dependent

Two events are Independent:

When two independent events A and B are occurring from the same sample space, the probability of two events happening at the same time is equal to that of A occurring times the probability of B occurring. The formula can summarize the same:

P (A Ո B) = P(A) *  P(B)

Two events are dependent:

When two dependent events A and B, are occurring from the same sample space, then the probability of two events happening at the same time is equal to the probability of A occurring times the probability of B occurring, given that A has already occurred. This is a conditional probability. The formula can summarize the same:

P (A Ո B) = P(A) *  P(B|A)

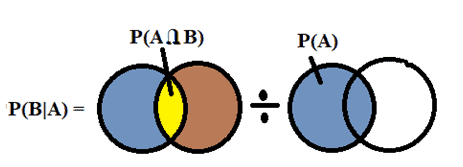
When Would You Use the Multiplication Law in a Six Sigma Project?

When the events have to occur together, then make use multiplication law of probability in Six Sigma projects.

A Six Sigma Example of the Multiplication Law

Two events are independent.

Example 1:  Two cars, Car A has a 60% chance of starting, and Car B has a 70% of starting. What is the probability of both cars starting simultaneously?

P (A Ո B) = P(A) *  P(B)

P = 0.6 * 0.7 = = 0.42

Two events are dependent.

Example 2:  Suppose A is the first event drawing King from a 52-card deck, and B is the second event drawing the King card from the rest of the cards. Then the probability is:

P (A Ո B) = P(A) *  P(B|A)

P (A Ո B) = 4/52 * 3/51 = 0.0045

Note: Here, the second denominator is only 51, as already one card has been drawn.

Mutually Exclusive Events

What are Mutually Exclusive Events?

Mutually exclusive events are things cannot both be true. In other words, they cannot occur at the same time.

When Would You Use Mutually Exclusivity in a Six Sigma Project?

Mutually exclusive events are used in Six Sigma projects. When one event occurs, it prevents the second from happening.

A Six Sigma Example of the Mutually Exclusive Probability

Example: When you flip a coin, what is the probability of getting both heads and tails simultaneously?

Probability of happening both had and tails same time:

P(head and tails) =0 or P(head Ո tails) =0

Example: What is the probability of rolling one 6-sided die and getting either a 3 or a 4?

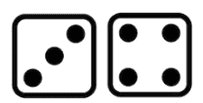
P (A or B) = P(A) + P(B)

P (3 or 4) = P(3) + P(4) = 1/6 + 1/6 = 1/3 = 33%

Complementary probability

Complementary probability is a statistical concept that refers to the probability of an event not occurring. It is often denoted by the symbol “P(A’).” A ′ represents the complement of A. The complement (A′) includes all outcomes in the sample space that are not the outcomes of event A. In other words, it consists of all outcomes in which event A does not occur.

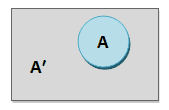
An event (A) and its complement (A′) are mutually exclusive, which means either event (A) or its complement (A′) will occur, not both at a time. Hence the complement rule is the sum of the probability of an event (A), and its complement (A′) is 1.

Probability of event occurring P(A) = Number of times the event happens / Total number of possible outcomes

Probability of event not occurring P(A′) = 1- (Number of times the event happens / Total number of possible outcomes)

P (A′) =1-P(A)

P (A) +P (A′) =1

For example, if the probability of rolling a 4 on a standard six-sided die is 1/6, then the complementary probability of not rolling a 4 is:

P(A’) = 1 – P(A) = 1 – 1/6 = 5/6

Therefore, the complementary probability of not rolling a 4 on a standard six-sided die is 5/6.

Example: When tossing a coin, if the event (A) is tails, then the complement (A′) is heads.
If you are throwing a die and the event (A) is even {2,4,6} then the complement(A′) is {1,3,5}.

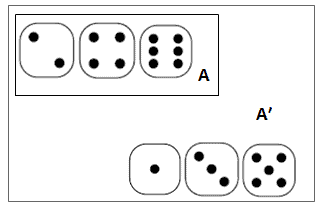
Complimentary probability is often used in statistical calculations and hypothesis testing, and it is a useful tool for understanding the relationship between different events and their probabilities.

Joint occurrence of events

The joint occurrence of events refers to the probability that two or more events will occur together. In other words, it is the probability that multiple events will happen simultaneously or in combination.

The joint probability of two events A and B can be denoted as P(A and B) and is calculated as the product of their individual probabilities.

P(A and B) = P(A) x P(B)

For example: Rolling a 4 on the die and flipping a coin, and getting tails. The probability of rolling on a die is 1/6, and the probability of flipping a coin and getting tails is 1/2. The joint probability of both events happening together is:

P(rolling a 4 and getting tails) = P(rolling a 4) x P(getting tails) = (1/6) x (1/2) = 1/12

Therefore, the joint probability of rolling a 4 and getting tails is 1/12.

Compound Events

What are Compound Events?

A compound event is when there is more than one possible outcome of an experiment. In other words, compound events are composed of two or more events. They consist of more than one point in the sample space.

When Would You Use Compound Events

Compound events are used when the outcome may have different probabilities, but they are all equally possible. Events that are chained together in a row.

A Six Sigma Example of Compound Events

Example: If two dice are tossed. What are the outcomes for the event that the sum of two dies is less than 5?

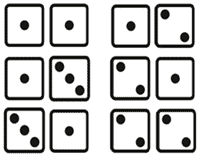
(1,1), (1,3), (3,1),(1,2), (2,1), and (2,2)

Independent Events

What Are Independent Events?

Events can be independent events when the outcome of one event does not influence another event’s outcome. In other words, each event is not affected by other events.

Whereas the dependent event is the probability of one event occurring that influences another event.

When Would You Use Independent Events in a Six Sigma Project?

Independent events are used in Six Sigma projects where one event does not connect with another event’s chance of occurring. The car mileage does not depend on the color of the car.

An Example of Independent Events

Example: What is the probability of rolling one 6-sided die thrice and getting a 2 on the first roll, 3 on the second roll, and a 4 on the third roll?

Since the roll of the second and third die can be anything–no matter what happens on the first roll–they are considered independent events.

P (A and B and C) = P(A) * P(B) * P(C)

P (2 and 3 and 4) = P(2) * P(3) * P(4) = 1/6 * 1/6 * 1/6 = 1/216

Sampling Without Replacement

Sampling Without Replacement is a probability question that is an example of using the Hypergeometric Distribution.

If the sample size was great compared to the population size, then we could use Binomial distribution to approximate.

Sampling Without Replacement Equation and Terms

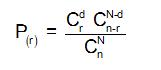
Remember that C(a / b) = a! / (b! * (a-b)!)

Population Size: N =

Sample Size: n =

Occurrences in sample: r = 0

Occurrences in population: d =

Sampling Without Replacement Example:

Five books are damaged out of a set of 15. What is the probability of selecting 3 undamaged books when you pull without replacing them?

First, compare the sample size to the population.

We see that the sample size (3) is small compared to the overall population size (15). Thus, we will use the hypergeometric distribution.

Next, we identify the terms:

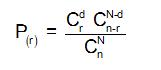
Population Size: N = 15

Sample Size: n = 3

Occurrences in sample: r = 0

Occurrences in population: d = 5

P = C(5/0) * C(10/3) / C(15/3)

C(a/b) = a! / (b! * (a-b)!)

P =  0.2637

Additional Basic Six Sigma Probability Resources

http://mi.eng.cam.ac.uk/~rwp/Maths/vid09/l9notes.pdf

https://www.mathgoodies.com/lessons/vol6/dependent_events

Basic Six Sigma Probability Videos