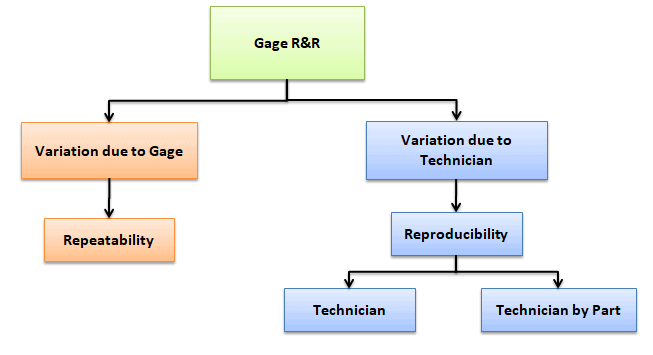
Gage Repeatability and Reproducibility are often referred to as Gage R&R. It’s a method to assess the repeatability and reproducibility of a measurement system. In other words, Gage R&R studies are carried out to discover how much of the process variation is due to the measurement system.

What is a Measurement System Analysis?

Measurement System Analysis (MSA) is a tool for analyzing the variation present in each inspection, measurement, and test equipment type. It is the system used to assess the quality of the measurement system.

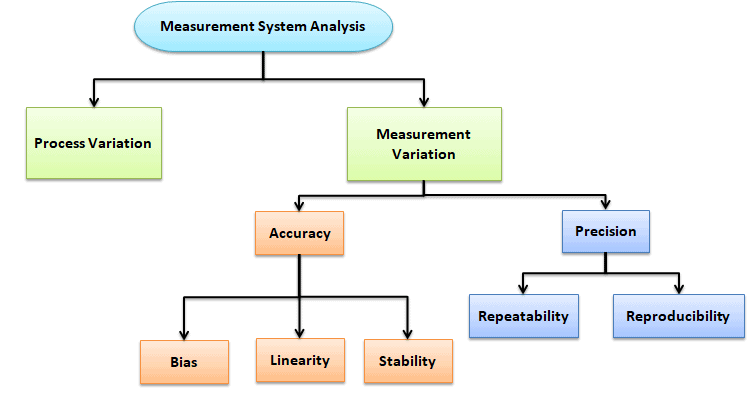
What is a Gage and Gage Repeatability and Reproducibility?

A gage, in this context, is a tool for measurement. A gage could be simple, like calipers and rulers. Or it could be a complex piece of machinery. It could even be a piece of software.

Gage R&R focuses on two key aspects of measurement:

  • Repeatability: Repeatability is the variation between successive measurements of the same part or trait by the same person using the same gage. In other words, how much variation do we see in measurements taken by the same person, on the same part, using the same tool?
  • Reproducibility: Reproducibility is the difference in the average of the measurements made by different people using the same instrument when measuring the identical characteristics on the same part. In other words, how much variation do we see in measurements taken by different people on the same part using the same tool?

Looking at these two metrics helps us to understand variation in our measurements. When we understand it, we can combat it.

Why is Gage Repeatability and Reproducibility Important?

Gage Repeatability and Reproducibility measure the amount of variability in measurements caused by the measurement system itself. Then, it compares this variability with the total to determine the actual variability of the measurement system. Gage R&R is very important when new workers are assigned; new tools are used, or any significant process changes.

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

For example, imagine a situation where our performance metrics show a serious problem in our manufacturing process. We spend a lot of time and money trying to fix it and improve the performance of a process. But we’d have noticed serious measurement variations if we’d spent some time looking at gage repeatability and reproducibility instead. The problem wasn’t in the process at all; it was in the measurements. Checking this first would have saved time, money, and stress.

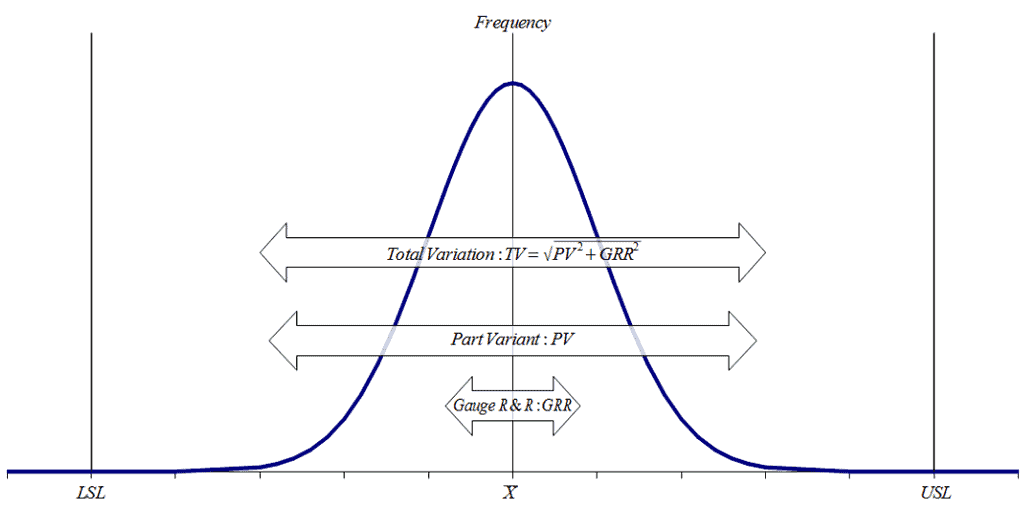
Gage Repeatability and Reproducibility (R&R)
Variation is made up of part and gage variation.
Image from Bo-ci-an under CC-BY-SA 3.0.

Types of Gage Repeatability and Reproducibility Study

Based on the available data and data type, there are basically three types of Gage R&R available:

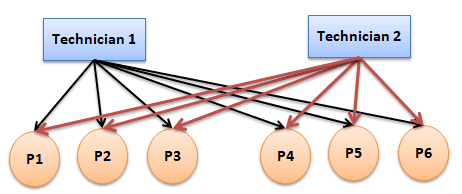
Crossed Gage R&R

Select crossed-gage R&R when each operator measures each part, and it must have a balanced design with random factors. It is used for non-destructive testing.

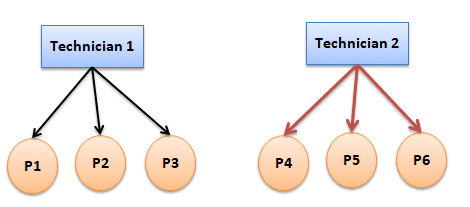
Gage Repeatability and Reproducibility (R&R)

Nested Gage R&R

Select nested gage R&R when only one operator measures each part. It is used for destructive testing. Since it is not crossed with other factors, it is called nested gage R&R. It must have a balanced design with random factors.

Expanded Gage R&R

Select expanded gage R&R when we need to include more factors (maximum of eight) than operator and part. Typically crossed and nested deal with only two factors (operator and part). Design can be balanced or unbalanced.

Gage Repeatability and Reproducibility (R&R)

Methods to Perform Gage Repeatability and Reproducibility Study

There are basically three methods that exist to perform Gage R&R:

  • Range method
  • Average and range method
  • Analysis of variance method

Range Method: The range method will provide a quick approximation of measurement variability but does not compute the measurement system repeatability and reproducibility separately.

Average and Range method: The Average and Range method quantifies the measurement system’s variability and provides repeatability, reproducibility, and part variation. Only crossed Gage R&R can be performed with the Average and Range method.

Analysis of Variance method: It is the most widely used and accurate method for measurement system repeatability and reproducibility. It also quantifies the variability of the interaction between the operator and the parts. Gage R&R (crossed, nested, and expanded) can be done with the ANOVA method.

Gage Repeatability and Reproducibility Using the Average and Range Method

The Average and Range method determines the total measurement system variability, which can be separated into components like repeatability, reproducibility, and part variation. Furthermore, this method requires multiple parts, operators, and trials. The Average and Range method is easy to compute; however, the ANOVA method is more accurate than the Average and Range method.

Example of Gage R&R using Average and Range method in a Six Sigma project

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step 1: Calibrate the gage(s) being used.

Step 2: Record a lot of different measurements taken by various people on the same units using the same gage. For each measurement, ensure that the unit, the person, and the gage are all recorded.

Step 3: Interpret your results to find sources of variation.

When you’ve finished your measurement recording, your results should look similar to this:

Gage Repeatability and Reproducibility (R&R)

Step 4: Find the range and mean for each combination

For Operator A and Part x , the Range = Max – Min = 0.33 – 0.29 = 0.04

Operator A and Part x, Mean = (0.29 + 0.31 + 0.33 + 0.32) /4 = 0.3125

Similarly, compute the range and mean for each combination.

Step5: Calculate the mean of means and range of each operator

For operator A: the mean of range = (0.04 + 0.04 + 0.04) /3 = 0.04

Similarly, the mean of mean of operator A = (0.3125 + 0.2875 + 0.2875) /3 = 0.2958

Similarly, compute the mean of range and mean of each operator

Gage Repeatability and Reproducibility (R&R)

Now find the total mean range and difference in means (Xdiff)

Total mean range = (0.04 + 0.02 + 0.01) /3 = 0.0233

Range of means = 0.2991 – 0.2958 = 0.0033

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step 6: Find the Repeatability- Equipment variation (EV)

EV = R̅*k1

  • Where R̅ = Total mean range = 0.0233
  • k1 =1/d2

To find the k1, we need the d2 value from the table

The d2 value can be found in the table based on the subgroup size and the number of combinations of parts and operators (g).

  • Subgroup size = number of trials = 4
  • Number of combinations of parts and operators (g) = 3 parts and 3 Operators = 3*3=9

Then, we have to see the d2 value from Tables 4 and 9

Gage Repeatability and Reproducibility (R&R)

refer d2 table

  • d2 =2.080
  • k1 =1/d2 = 1 /2.080 = 0.480
  • EV= R̅ *k1= 0.0233 *0.480 = 0.0112

Step7: Find the Reproducibility– Appraiser Variation (AV)

  • x̅diff is the range of means = 0.0033
  • Where n = number of parts = 3
  • r = number of trials = 4

To find the k2, we need the d2 value from the table

The d2 value can be found in the table based on the number of parts and the number of combinations of parts and operators (g)

  • Number of parts =3
  • Number of combinations of parts and operators (g) = 3 parts and 3 Operators = 3*3=9
  • d2 =1.718
  • k2=1/d2 = 1 /1.718 = 0.5820

If the number is negative, set AV=0

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step8: Calculate Gage R&R

Then, interpret the results. According to the Automotive Industry Action Group (AIAG), below are the guidelines for measurement system assessment using %GRR.

Since the Total Gage R&R is 1.12%, it is in the green zone. So, it is considered to be an acceptable measurement system based on application and cost factors.

Gage_RR_Average_Range_TemplateDownload

How to Measure Gage Repeatability and Reproducibility Using ANOVA Method

  • Measuring the Gage R&R with a minimum of 10 parts is recommended.
  • Select two technicians to measure the parts.
  • Have each technician measure each part 2 or 3 times.
  • It is recommended that each technician take three measurements per part.
  • Collect the measurements of parts in random order and measure the overall average of all measurements (x̿).
  • t= number of technicians
  • r= number of trials or replications
  • p= number of parts

Step 1: Calculate the technician sum of squares

This provides the sum of squares by determining the squared deviations between the technician average and the overall average.

Step 2: Compute the parts sum of squares

It provides the sum of squares by determining the squared deviations between the part’s average and the overall average.

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step 3: Calculate the total sum of squares

SSTotal = SSTechnician + SSPart + SSTech*Part + SSEquipment

It is the squared deviation of each individual result from the overall average.

Gage Repeatability and Reproducibility (R&R)

Step 4: Compute Equipment within the sum of squares

It uses the deviation of all trials for a given part and given technician from the average for that part and technician. 

Step 5: Find the interaction sum of squares

SSTotal = SSTechnician + SSParts + SSTechnician*Part + SSEquipment

SSTechnician*Part = SSTotal – (SSTechnician + SSPart+ SSEquipment)

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step 6: Create an ANOVA table

Gage Repeatability and Reproducibility (R&R)

Step 7: Evaluate repeatability, technician, part, and interaction variance

  • σ2 Repeatability = MSEquipment
  • σ2 TechnicianxPart = (MSTechnicianxPart – σ2 Repeatability)/ number of trials
  • And, σ2 Part = (MSPart – MSTechnicianxPart)/ (number of trials * number of technicians)
  • σ2 Technician = (MSTechnician – MSTechnicianxPart)/ (number of trials * number of parts)

If any of the values are negative, then consider it as zero.

Step 8: Compute Gage R&R and interpret the results

  • Gage R&R = σ2 Repeatability  + σ2 Technician
  • Equipment Variation (Reliability) = σ2 Repeatability 
  • Technician Variation (Reproducibility) = σ2 Technician + σ2 TechnicianxPart
  • Part to Part = σ2 Part
  • Total Variation = σ2 Repeatability + σ2 Part+ σ2 Technician+ σ2 TechnicianxPart

Calculate the % Contribution Variance and interpret the results. Below are the criteria for acceptance of Gage R&R.

Then, find the standard deviation and % study variance. Interpret the results. According to the Automotive Industry Action Group (AIAG), below are the guidelines for the measurement system assessment using % GRR.

Gage Repeatability and Reproducibility (R&R)

What is the Number of Distinct Categories (NDC)

The number of distinct categories is a metric. In gage R&R, the goal is to identify the measurement system’s ability to detect a difference in the measured characteristic. It represents the number of non-overlapping confidence intervals that span the range of product variation.

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

The formula for the number of distinct categories

Number of distinct categories = (Standard deviations for parts / standard deviation for gage) * √2

So, the number of categories depends on the ratio of the variability in the measuring parts and the variability in the measurement system.

Guidelines for the number of distinct categories

According to the Automotive Industry Action Group (AIAG), the number of distinct categories should be greater than 5 for an adequate measuring system.

  • >=5: Adequate measuring system   
  • =2:    Data can be divided into two: say Low and High          
  • =3:    Data can be divided into three: say Low, Medium, and High  
  • <2:    Measurement system of no value for controlling the system 

Example of Gage Repeatability and Reproducibility (R&R) using ANOVA method in a Six Sigma project

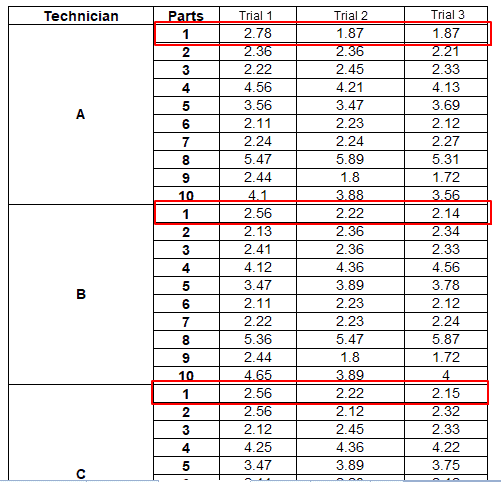
Example: A testing engineer selected ten parts representing the expected range of process variation. Three technicians measured the ten parts three times a part in random. Assess the measurement system Gage R&R.

Gage Repeatability and Reproducibility (R&R)
  • t = number of technicians = 3
  • r = number of trials or replications = 3
  • p = number of parts = 10

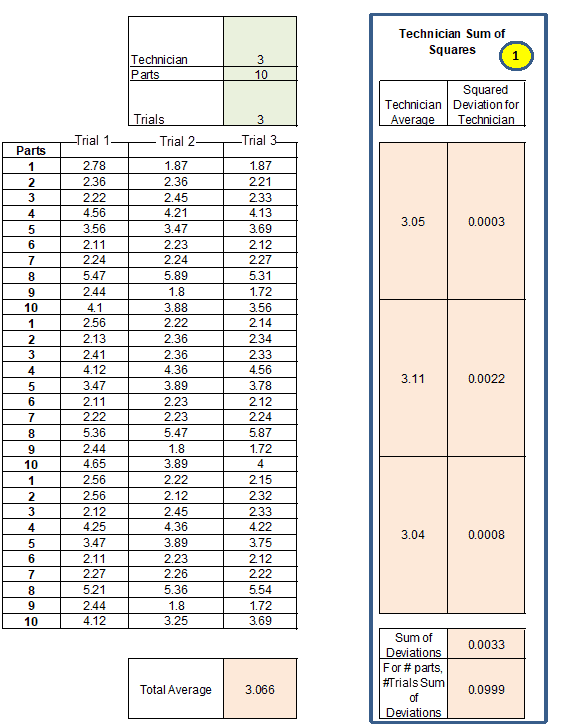
Average of all the measurements = (2.78+1.87+1.87+2.36+2.36+2.21+……….+2.44+1.8+1.72+4.12+3.25+3.69)/90= 3.066

Step 1: Calculate the technician sum of squares

Calculate the average measurement for each technician

For technician A: Average value of 3 trials for ten parts = ((2.78+1.87+1.87+2.36+2.36+2.21+……….+4.1+3.88+3.56)/30 = 3.05

Calculate the squared deviation of each technician: squared deviations between the technician average and the overall average

For technician A: (3.05-3.066)2 =0.0003

Similarly, calculate for technicians B and C

Add all squared deviation for technicians = 0.0003+0.0022+0.0008=0.0033

For the ten parts and three trials, the sum of deviations = 3*10*0.0033 =0.0999

Gage Repeatability and Reproducibility (R&R)

Step 2: Calculate the parts sum of squares

Calculate the average of measurement for each part for all the trials for part 1: (2.78+1.87+1.87+2.56+2.22+2.14+2.56+2.22+2.15)/9=2.263

Calculate the squared deviation of each part: squared deviations of each part and the overall average.

For part 1: (2.263-3.066)2 =0.644

Similarly, calculate values for 10 parts

Add all squared deviations for 10 parts = 0.644+0.577+0.537+1.542+0.357+0.833+0.677+5.914+1.165+0.703=12.9477

For 3 trials and 3 technicians, the sum of the deviations = 3*3*12.9477 =116.5294

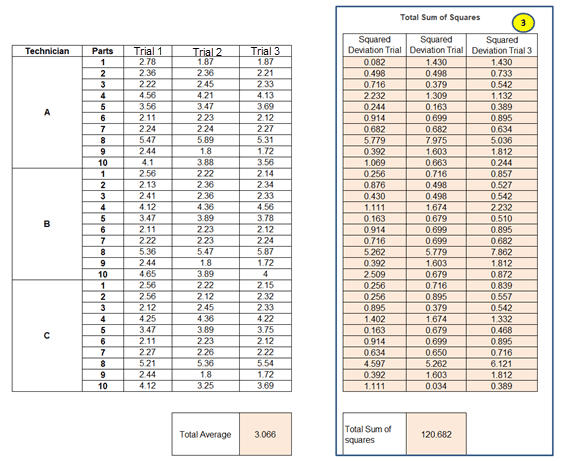
Step 3: Calculate the total sum of squares

Calculate the squared deviation for each individual result from the overall average.

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

For the first part of trial 1: (2.78-3.066)2 = 0.082

Similarly, conduct for all the 90 trials and sum the squared deviation of 3 trials = 0.082+1.430+1.430+……..+1.111+0.034+0.389 =120.682

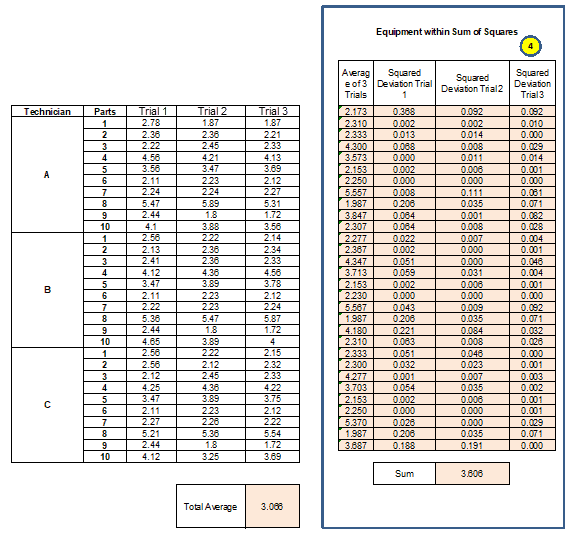
Step 4: Compute Equipment within the sum of squares

It uses the deviation of all trials for a given part and given technician from the average for that part and technician.

Take the average of the first part of the first technician’s three trials = (2.78+1.87+1.87)/3 =2.173

Calculate the Squared Deviation Trial 1 for first part = (2.78-2.173)2 = 0.368

Similarly, calculate the squared deviation for all trials for each part.

Sum of 90 values = 0.368+0.092+0.092+…………………+0.188+0.191+0.000=3.606

Step 5: Find the interaction sum of squares

SSTechnician*Part = SSTotal – (SSTechnician + SSPart+ SSEquipment)

SSTechnician*Part = 120.682 – (0.0999 + 116.5294+ 3.606) =0.447

Step 6: Create an ANOVA table

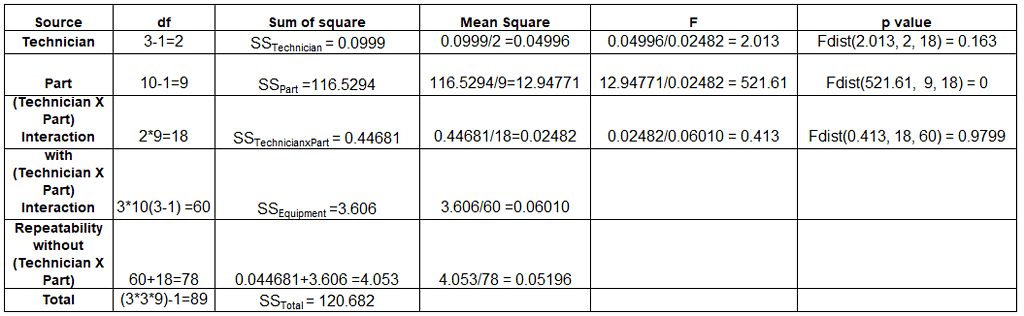
Since the p-value for interaction is more than 0.05, we need to consider the repeatability without interaction values.

Step 7: Evaluate repeatability, technician, part, and interaction variance

  • σ2 Repeatability = MSEquipment =0.05196
  • Then, σ2 TechnicianxPart = (MSTechnicianxPart – σ2 Repeatability)/ number of trials = (0.02482-0.05196)/3 = -0.00904 =0
  • σ2 Part = (MSPart – MSTechnicianxPart)/ (number of trials*number of technician) = (12.9477-0.05196)/(3*3) = 1.4328
  • σ2 Technician = (MSTechnician – MSTechnicianxPart)/ (number of trials*number of part) =(0.04996-0.05196)/(10*3) = -0.00006667 =0
Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Step 8: Compute Gage R&R and interpret the results

  • Gage R&R = σ2 Repeatability  + σ2 Technician =0.05196+0 = 0.05196
  • Equipment Variation (Reliability) = σ2 Repeatability  =0.05196
  • Technician Variation (Reproducibility) = σ2 Technician + σ2 TechnicianxPart = 0+0 =0
  • Part to Part = σ2 Part=1.4328
  • Total Variation = σ2 Repeatability + σ2 Part+ σ2 Technician+ σ2 TechnicianxPart = 0.05196+1.4328+0+0 = 1.4848

From the above values, compute the % contribution variance.

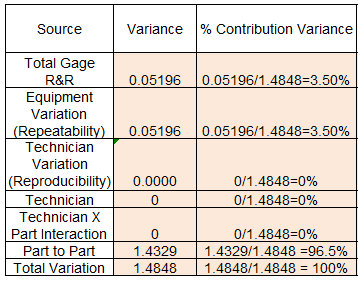
Gage Repeatability and Reproducibility (R&R)
Gage Repeatability and Reproducibility (R&R)

Since the Total Gage R&R is 3.5%, it is in the yellow zone. So it may be acceptable depending on the application and cost factors, but the team needs to improve it further.

Find the standard deviation and % study variance.

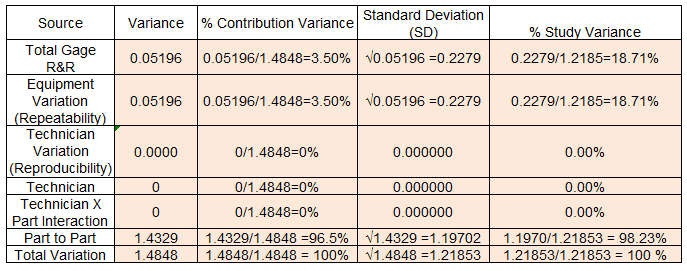
According to the Automotive Industry Action Group (AIAG) measurement system assessment using %GRR.

Since the Total Gage R&R is 18.71%, it is in the yellow zone. So it may be acceptable depending on the application and cost factors, but the team needs to improve it further.

Don’t like Ads? Neither do I. If you’re a member, just log in to avoid ads. If you’re not a member, what are you waiting for? Sign up here!

Calculate the number of distinct categories (NDC)

According to the Automotive Industry Action Group (AIAG), the number of distinct categories should be greater than 5 for an adequate measuring system.

Number of distinct categories =(Standard deviations for parts / standard deviation for gage) * √2 = (1.9702 /0.2279) * √2 = 7

Gage Repeatability and Reproducibility ANOVA Excel Template

Unlock Additional Members-only Content!

To unlock additional content, please upgrade now to a full membership.
Upgrade to a Full Membership
If you are a member, you can log in here.

Thank You for being a Member!

Here’s some of the bonus content that is only available to you as a paying member.

Gage_RR_ANOVA_TemplateDownload

Gage Repeatability and Reproducibility using Minitab

Step 1: Copy the data in the Minitab sheet

Gage Repeatability and Reproducibility (R&R)

Step2: Select Stat –> Quality Tools –> Gage Study –> Gage R&R (Crossed)

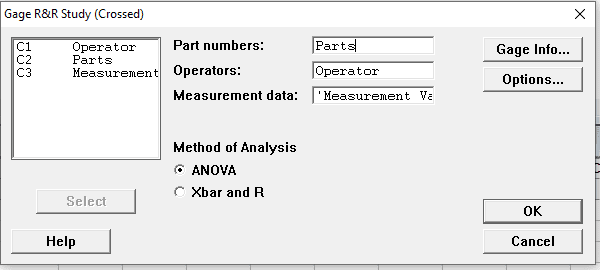
Select Part numbers, Operator, and Measurement data, and select the ANOVA method.

Under options: Enter process tolerance, the default alpha to remove interaction term would be 0.25. click on ok.

Step 3: Interpretation of results (session window)

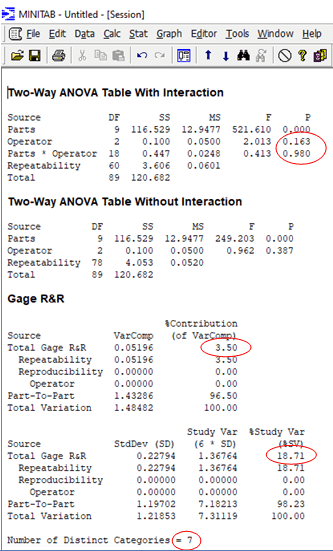
Gage Repeatability and Reproducibility (R&R)
  • The p-value for the operator (0.163) is greater than 0.05.
  • The p-value for Parts * Operator (0.98) is greater than 0.05. Hence, Minitab ignores the values and considers the values in the without interaction table.
  • The part-to-part variation is 96.5x, which is much greater than the total Gage R&R (3.5%). This tells us that there is a lot of variation between the parts.
  • Total Gage R&R is 3.5%. So, it may be acceptable depending on the application and cost factors, but there is a scope for improvement.
  • Similarly, in the % study variance, the total Gage R&R is 18.71%. According to the AIAG, it may be acceptable depending on the application and cost factors, but the team needs to improve it further.
  • The number of distinct categories is 7, which is greater than the acceptable number of 5.

Step 4: Interpretation of results (graphs window)

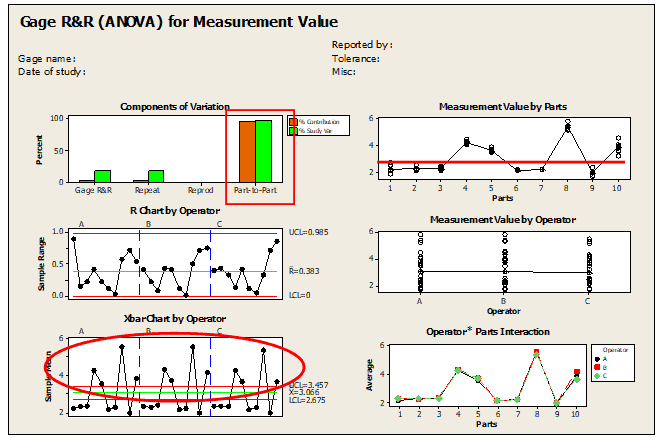
Gage Repeatability and Reproducibility (R&R)
  • First Graph- Components of Variation: It clearly shows too much variation is between the part to part, but not due to Gage R&R.
  • Second Graph- Measurement values by parts: Clearly indicate the variation between the parts.
  • Third Graph- R chart by the operator: All the values are within control limits.
  • Fourth Graph – Measurement value by the operator: The difference between operators is small.
  • Fifth Graph – X bar chart by the operator: Most of the points are outside of control limits. Hence, it indicates that variation is basically due to the parts.
  • Sixth Graph – Operator * Parts Interaction: There is not much difference between the operators, and also there is no interaction between the parts and the operator.

Videos of Gage Repeatability and Reproducibility Charts

Video: How to set up a Gage R&R study

Gage R&R Definitions

Precision

  • Getting consistent results repeatedly.
  • The repeatability of the gage.

Accuracy

  • Unbiased true values are obtained.
  • Must be assured before an R&R can be performed.
  • This is why we calibrate.

Sensitivity

  • Ability to detect differences in measurement.

Reproducibility

  • We compare the results of different operators at different times.
  • We examine variation between the averages of each operator.

Repeatability

  • We look at the variation between individual operators.
  • We look at the variation within their readings.

Traceability

  • The accuracy of a measuring instrument mapped to US national standards.

Attribute Gage Repeatability and Reproducibility

Attribute data is a form of discrete data. Counts rather than measurements denote it. Such as Yes or no, Pass or fail and GO or no GO. It is a complex measurement system because human judgment is involved in most cases. Attribute gage R&R helps to perform such analysis. Ideally, the target for gage R&R would be 100%; however, getting 100% is not always possible. Hence, anything above 90% percent is acceptable.

Attribute Gage R&R Example in a Six Sigma project

  • To measure the Gage R&R, it is recommended to measure a minimum of 20 to 30 parts
  • Select 2-3 technicians to measure the parts
  • Have each technician measure each part 2 or 3 times

Step 1: Take master appraiser readings

Step 2: Select three Operators and have them categorize each transaction (2 trials) without knowing what the master readings are.

You will use these trials as a sample.

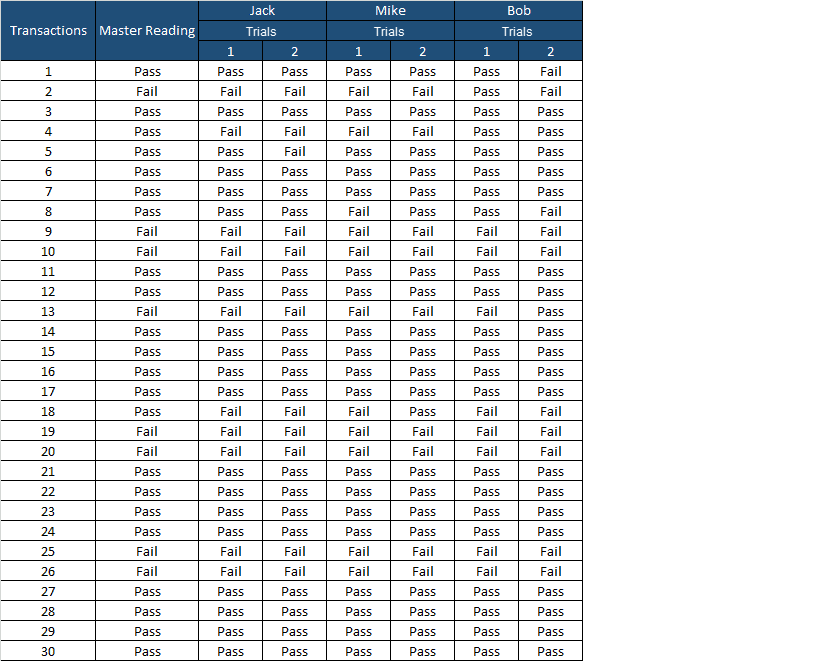
Step 3: Repeatability of the operator- count the number of times the operator readings agree (between two trials). Divide the total agreed number by the total transactions to obtain the percentage of agreement.

  • In Excel, we can use the “IF” formula to check that both the trial data sets are agreed upon (C5 and D5 cells). If both are agreed, use 1; otherwise, 0. For Example: =IF(C5=D5,1,0)
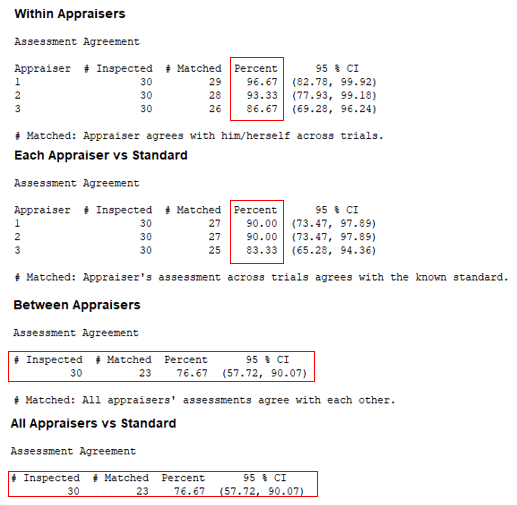
  • Operator Jack: Out of 30 Transactions, 29 values are agreed upon between trial 1 and trial 2. So, repeatability of Jack =29/30 = 96.7%

Step 4: Compute each operator vs. Master readings

  • Now compare Jack’s two trials values with Master transactions
  • In Excel, we can use the “IF” formula to check both the trial data sets agree with the Master reading (C5, D5, and B5 cells). If both are agreed, use 1; otherwise, 0. For Example: =IF(AND(C5=B5,D5=B5,1,0).
  • Operator Jack: Out of 30 Transactions, 27 values are agreed upon between trial 1, trial 2, and the master readings. So, the % agreement of Jack’s data set with the master transactions =27/30 = 90.0%.

Similarly, compute for the other the operator’s repeatability and agreement with master readings.

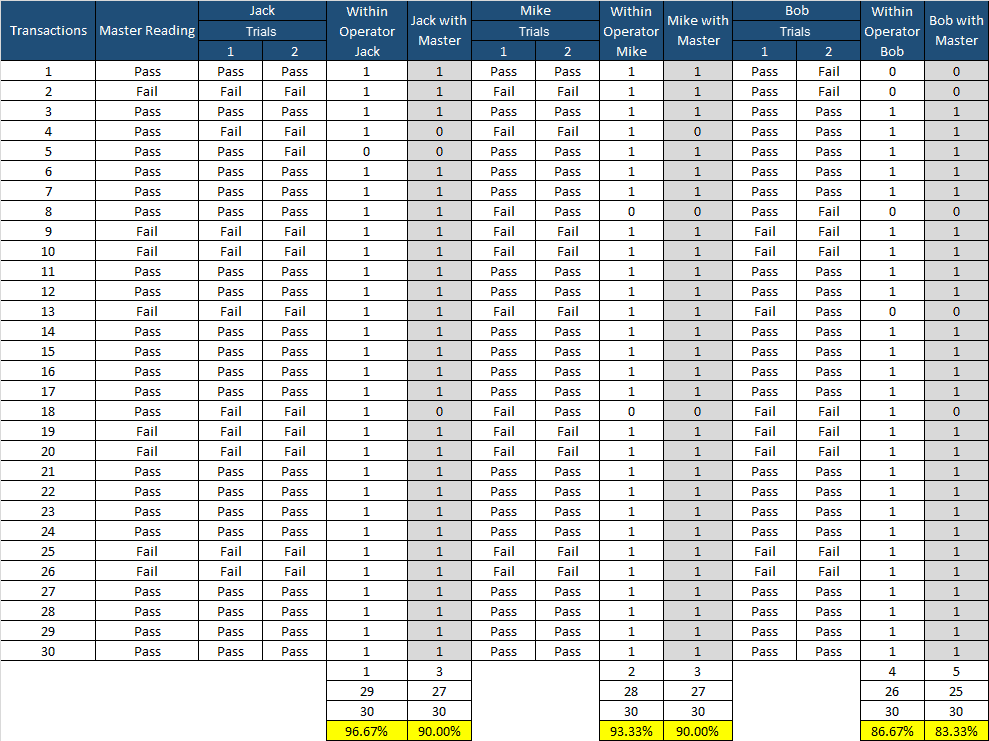
Step 5: Compute reproducibility between operators

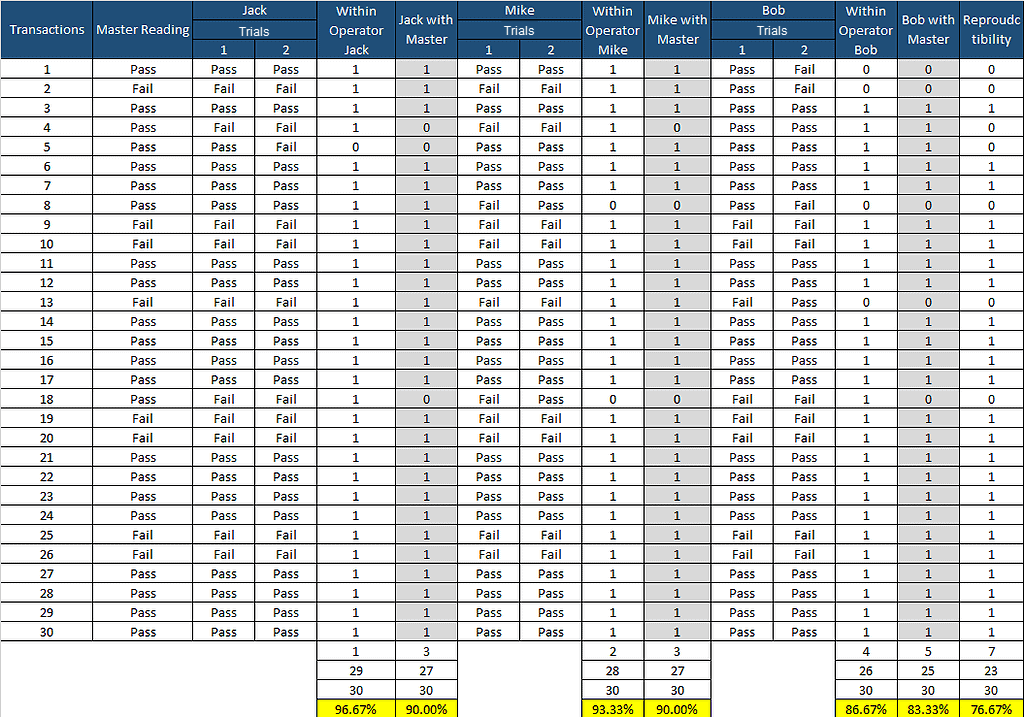
  • In Excel, we can use the “IF” formula to check reproducibility between operators (C5, D5, G5, H5, K5, and L5 cells). If all are agreed, use 1; otherwise, 0. For Example: =IF(AND(C5=D5,C5=G5,C5=H5,C5=K5,C5=L5,1,0)
  • Reproducibility: Out of 30 Transactions, 23 values are agreed upon between 3 operators. So, the % Reproducibility =23/30 = 76.7%.

Step 6: Overall Effectiveness (All operators vs. Standard) – Compute the percentage of the time that all the operator’s transactions are agreed upon among each other and with the master transaction.

  • In Excel, we can use the “IF” formula to check overall effectiveness (C5, D5, G5, H5, K5, L5, and B5 cells). If all are agreed, use 1; otherwise, 0. For Example: =IF(AND(B5=C5,B5=D5,B5=G5,B5=H5,B5=K5,B5=L5,1,0)
  • Overall Effectiveness: Out of 30 Transactions, 23 values are agreed upon between 3 operators. So, the % Overall Effectiveness =23/30 = 76.7%

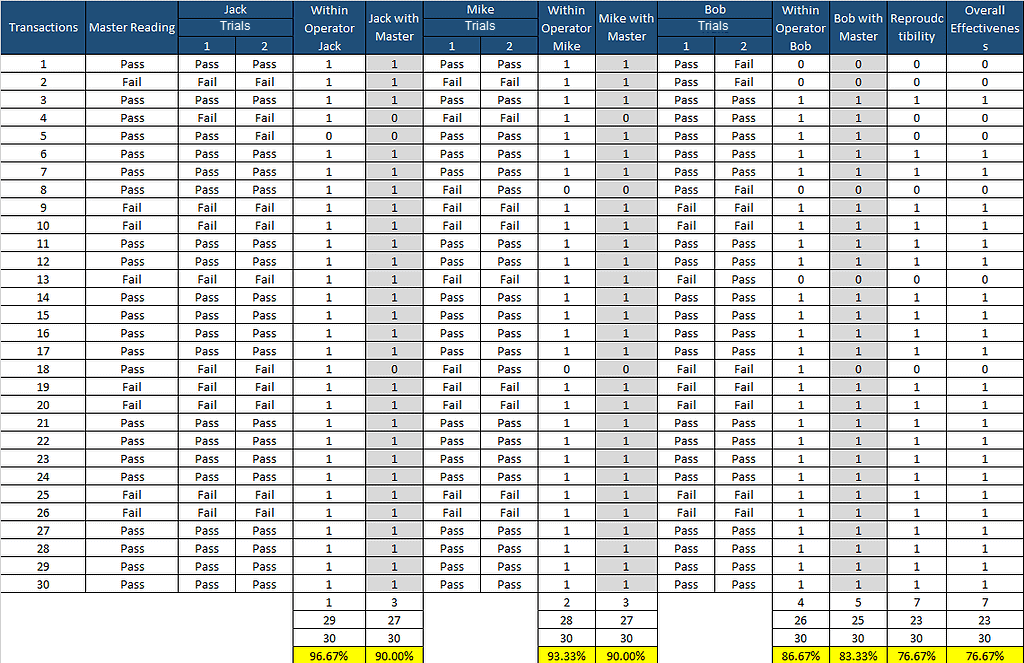
Step7: Conclusions

As per AIAG acceptance criteria of attribute data MSA:

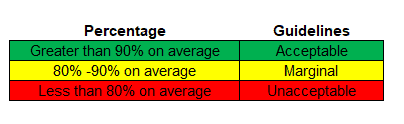
MSA will be failed as the overall efficiency is only 76.7%. MSA Should be greater than 90%. We need to take the appropriate actions for improvement.

Attribute_Gage_R_RDownload

Attribute Gage R&R using Minitab

Step 1: Copy the data in the Minitab sheet

Step2: Select Stat –> Quality Tools –>Attribute Agreement Analysis

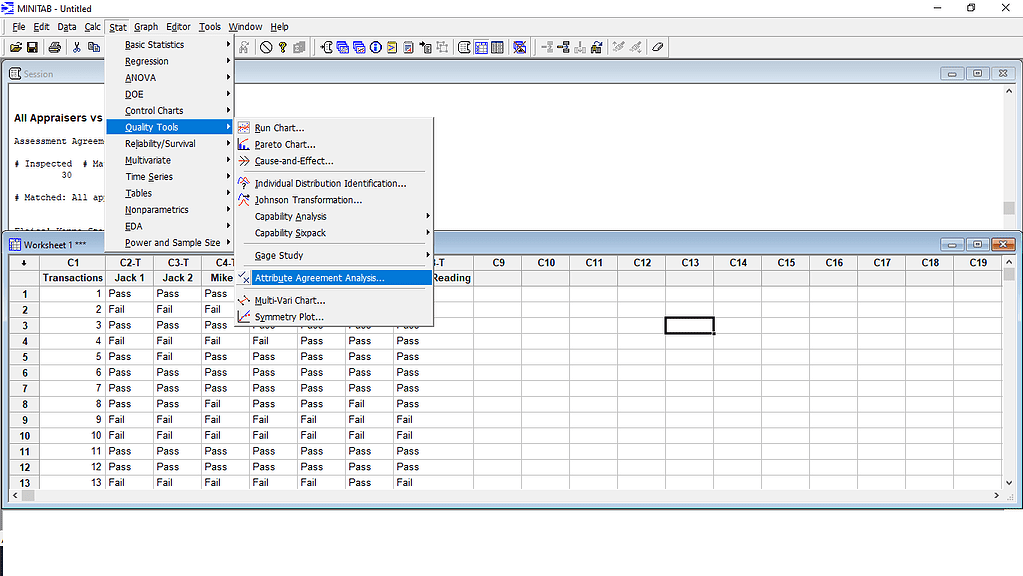
Select the Multiple Columns option and include Operator trials 1 and 2 data, add the number of appraisers as 3, and the number of trials as 2. Add the master values under “Known standard/attribute.”

Step 3: Interpretation of results (session window)

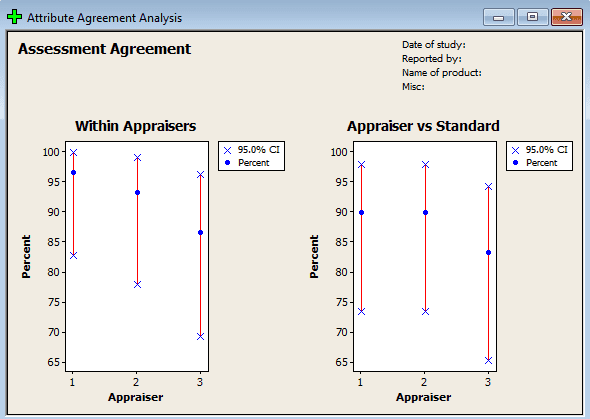
Additional Attribute Gage R&R Articles

What You Need to Know for Your Six Sigma Exam

Green Belts

The IASSC Green Belt BOK lists understanding Gage R&R under their Measure Phase.

The ASQ Green Belt BOK describes the following requirements for Gage R&R under Measurement system analysis.

Calculate, analyze, and interpret measurement system capability using repeatability and reproducibility (GR&R), measurement correlation, bias, linearity, percent agreement, and precision/tolerance (P/T). (Evaluate)

Black Belts

The IASSC Black Belt BOK lists understanding Gage R&R under their Measure Phase.

The ASQ Black Belt BOK describes the following requirements for Gage R&R under Measurement system analysis.

Use various analytical methods (e.g., repeatability and reproducibility (R&R), correlation, bias, linearity, precision to tolerance, percent agreement, etc.) to analyze and interpret measurement system capability for variables and attributes measurement systems. (Evaluate)

When you’re ready, there are a few ways I can help:

First, join 30,000+ other Six Sigma professionals by subscribing to my email newsletter. A short read every Monday to start your work week off correctly. Always free.

—

If you’re looking to pass your Six Sigma Green Belt or Black Belt exams, I’d recommend starting with my affordable study guide:

1)→ 🟢Pass Your Six Sigma Green Belt​​

2)→ ⚫Pass Your Six Sigma Black Belt ​​​

You’ve spent so much effort learning Lean Six Sigma. Why leave passing your certification exam up to chance? This comprehensive study guide offers 1,000+ exam-like questions for Green Belts (2,000+ for Black Belts) with full answer walkthroughs, access to instructors, detailed study material, and more.

​ Join 10,000+ students here. 

Authors

Comments (65)

You you help to explain how to calculate Gage R & R for true position (with x and y values), please? I dont see any article discuss about this

Thank you very much!

Reply

Sir can you explain why (EV)2 / (n * r)) gets subtracted from (Xdiff * k2)2 in reproducibility calculation ,in the formula?

Please help to understand.

Reply

(EV)2 / (n * r) is a measure of repeatability for the formula. If you try to take reproducibility data in a Gage R&R study and analyze it in a spreadsheet without these formulas, you find a problem where the reproducibility includes repeatability. So this is some really smart statistician’s way of removing repeatability from reproducibility.

Reply

Hi Nguyen, under what circumstances would I get the same figure for % variation and repeatability?

Study Var %Study Var
Source StdDev (SD) (6 × SD) (%SV)
Total Gage R&R 1.3378 8.027 3.80
Repeatability 1.3378 8.027 3.80
Reproducibility 0.0000 0.000 0.00
Part-To-Part 35.2077 211.246 99.93
Total Variation 35.2331 211.399 100.00

Reply

You’re right Manish. I should have clearly specified that the repeatability is solely for each individual calculation and that the reproducability was calculated across all operators.

Reply

Repeatability isn’t just gauge error. It is the ability of an operator to get the same value measuring the same part with the same gage.

You use multiple operators in the repeatability calculation because different operators will have different repeatability. It all gets lumped together in the calculations, but you should be looking at more than just the calculations. If you look at the control charts, specifically control charts staged by operator, you can see if one operator is more or less consistent than the others. When you calculate reproducibility in this manner, using the range of the operator averages, are looking for the ability of the operators to get the same average value in the measurement. One operator might get 2, 4, 6, and the second get 3,4,5. They both average to 4 for the reproducibility calculation, but they have two different repeatability’s.

Where you will see this show up often is when measurements have a ‘feel’ to them. Take measuring a cylinder with a caliper for instance. One operator may be more consistent with the pressure on angle they hold the caliper at. That operator is more repeatable within their own measurements. On a depth gage, even if you have them use the ratchet you can get different results for repeatability for different operator. Run it down with one click vs. 3 clicks and you can get different results. Run it down fast vs. slow and you can get different results. If you have repeatability issues from the calculations, you can look at the staged control charts, see if it is a single operator driving it up and then witness their technique. It is possible that retraining is needed, or better work instructions.

Basically, as long as you have an operator involved in the measurement, you won’t have a repeatability value that is not influenced by operator, which is why multiples are included.

Reply

Trying to find the answer for the IASSC Lean Six Sigma Black Belt.
A Gage R & R Analysis is analyzing which two:
A. Reliability
B. Replication
C. R Value
D. Repeatability

I know that Repeatability is one of the answer.

Reply

how you calculate d2 is not clear? how d2 is depend on m and g variables?
please explain clearly.

Reply

Referring to the statistical table for d2, the number of subgroups (K) you will have in a study like this is your (number of operators)x(number of parts). This can be visually seen by looking at the second table in the example above. There are three operators and three parts which gives nine rows in the table and thus leaves us with nine ranges and nine operator means. That equates to nine subgroups.

When considering repeatability (EV) for determining subgroup size, consider: how many measurements did each operator repeat? The operator repeats a number of measurements equal to the number of trials and this directly affects how many data points go into each range which then affects the repeatability. Therefore, the subgroup size for EV is n=number of trials.

When considering reproducibility (AV), consider: how many measurements does each appraiser make? That will be the number of parts, therefore, n=number of parts.

Reply

Hi Ted
in case of GR&R study on operator. input data is by operator and result is pass or fail, what is a best way to calculate GR&R?

Reply

Hi, how do we then use these results, gage r and r, repeatability and reproducibility to determine the test limits?

Reply

How you obtained the d2 is not clear. I looked in the table and it does not clearly make sense. The d2 used in the example above was 2.079. This number is not anywhere on the table you added a link to. Could you please explain how the number was found?

Thanks!!

Reply

Related comment,
How to obtain the d2 is not clear. Mostly because the usage of g is not explained anywhere.
Also, I would like to note that the referenced table is marked as “old” on the file name. Constants would not change during years, and new one has much less explanation, but still I would think that would be preferred to use newer material.

Please, explain the usage of g to obtain d2.

Reply

Hi folks! Regarding the d2 lookup…

You need a d2 table that allows for more than one subgroup (that’s your ‘g’ value), or your calculation will be off. I used the d2 table from the Measurement Systems Analysis Reference Manual, Third Edition. If you don’t have a copy just lying around waiting to be consulted, there’s a PDF copy (I assume the company has permission to disseminate) at http://parsetraining.com/wp-content/uploads/2018/11/MSAmanual.pdf – Appendix C.

Alternatively, use the search term ‘d2 table subgroups’ in a search engine like Google and you’ll find a number of applicable tables that people have published. This one has rounded to three decimal places, which should be fine for the vast majority of calculations: https://andrewmilivojevich.com/d2-values-for-the-distribution-of-the-average-range/

Apologies for the misleading table link. I’ve amended that now.

Cheers,
Naomi

Reply

Hi Ibrar,

Look at some of the comments above – especially Naomi’s.

We’ll add more depth to this article in the future but for now that’s a good start.

Best, Ted.

Reply

I have a set of data
k = 3
n = 5
r = 10
I calculated thru ANOVA, I get 80.2% GRR.
But when I calculated thru AVERAGES and RANGES, I get 27.7%
Please help figure out what I did wrong. Thanks!

Reply

Hi Richard,

It’s difficult to pinpoint without seeing all of your calculations. If I were to guess, it would be that perhaps you are trying to do a kind of R&R (there are 3 main types) that isn’t applicable to both the range and ANOVA method.

To my understanding, only the crossed R&R can be used in both cases. After that, there might be a minor math error. The answers would be different, but unlikely to be that far off.

Looking forward to hearing what you discover.

Best, Ted.

Reply

One thing that is super unclear to me is Gage R&R. I don’t think there is enough on the R&R page given how many questions are asked about it on the quizzes and reviews. For example, I had a question where I was given R-Bar and K1, but after reading Gage R&R and doing a page search for “k1” the only result was a comment telling us to refer to Naomi’s comment which covered D-tables. I’m still not really sure how to do it.

Reply

Hello everyone, please note in the example above, everything works well until the calculation for RR. At that point, the RR value is treated as a percentage. If you go back to the figure above showing how to find percent %R&R the formula for RR and %R&R are not the same. In order to find %R&R, the total variation (TV), is needed. In order to find total variation, the part variation is needed. Part variation is best determined based on historical production data, but lacking that it can be estimated in the following way: PV=jR, where R is the range of the part averages and j, is dependent on the number of parts in the study. For the example above, the overall average of part x is 0.3075, y is 0.2875, and z is 0.2975. The R is then 0.02. j=5.15/d2 where k=1 and n=number of parts. (j=6/d2 might also be used) For this example, j=2.70. Part variation for this example is 0.054, which using the formulas above gives us a total variation of 0.055. Finally, if the analysis is continued, we will find %R&R= 20.4% which is very different than 1.12%. Putting the data into the crossed MSA option in Minitab will show that the measurement system is not acceptable. Regards to everyone, take care and be safe.

Reply

Hello, my question is regarding the set up for the actual Gage R&R Study in regards to chemical manufacturing – example provided.
A plant makes hundreds of different types of batches/materials that use various gages to measure product specification. For example, say we’re interested in viscosity. When providing samples for the study, should the samples be comprised of different materials (which will have different average values for viscosity) OR should the samples be comprised of one material type, but different lots (different production dates, but should have the same average values for viscosity)?

Reply

Hello Brittany,

Gage repeatability and reproducibility (GR&R) is defined as the process used to evaluate a gauging instrument’s accuracy by ensuring its measurements are repeatable and reproducible.

• Repeatability: variability in repeated measurements when the same person measures the same item(s) repeatedly with the same instrument.
• Reproducibility: variability in repeated measurements when different people measure the same item(s) repeatedly with the same instrument.

It does not matter the same material or different material unless it provides the same values if the same person measures repeatedly or different people measure the same item repeatedly. Based on the scenario, we need to select crossed or nested Gage R&R.

For example, suppose the first sample is 1.2 Pa.S and another sample 2.3 Pa.S. It should give the same value if the same person measures repeatedly or different people measure the same item repeatedly.

But please note that when conducting GRR, assuming the specimens in the study do not change in physical properties that can affect the measurements over time.

Thanks

Reply

Hello,
While explaining the first step of the anova method you claim (3.05-3.066)^2 = .003. This seems to be a print error as It should be .0003 (.000256 rounded up). You also use .0003 later on in the image and cannot get the squared deviation sum to be .0033 with .003.

Thanks

Reply

Yes, Max. It is 0.0003 (.000256 rounded up), a print error. However, the calculation is correct as you indicated.

Thanks

Reply

This was a rally confusing article when it came to the math. The math does not add up especially when you try and do the AV portion with the numbers you have plugged in. I have done it multiple times/ways and it just doesn’t come out with your numbers.

Reply

Hello Ronald Adams,

We have included an excel template with detailed explanations and formulas in the article. Members can download it from our site.

Thanks

Reply

Your example of how to calculate Gage R&R using ANOVA is extremely confusing. The variable “MSTechnicianxPart” is used VERY liberally and appear multiple times with different values in your calculations. Additionally, the image uploaded for the ANOVA table is truncated on the first column. Would you be able to clarify the actual calculations and make it more clear which variables are being used?

Reply

He Ted. First Congratulations on a very clear and informative article. I had one query:
You have defined the F value for Tech as (MS Tech/MTech*Part ). Likewise for MS Part. Further the values obtained manually match the Minitab results.

I ran the ANOVA thru Excel 2 factor with replication successfully and all the SS and MS values matched. However the F values for Tech and Part did not match. The values obtained are from Excel are 0.831 and 215.44 for Tech and Part respectively. The F value for (Tech*Part) matches excel where the denominator used by you and Excel are the same – i.e. MSequipment. I checked various statistics texts* (see one below) and found that the denominator is supposed to be “The residuals” ( i.e. SS equipment in this case) for all three items – Parts, Tech and Parts*Tech. This is what Excel has used. I would be grateful if you can you give your comments on the above. Regards, Niraj Goyal

* F Value Definition: The F ratios are calculated by the Mean sum of squares of an entity and the mean sum of residuals squares.
Anova Two Factor with Replication [With Comparison] – upGrad
http://www.upgrad.com/blog/anova-two-factor-with-replication/
http://www.upgrad.com/blog/anova-two-factor-with-replication/

Reply

Hi Niraj Goyal,

The table is correct if you keep the interaction term in the model, as this article does. The F-values for the technician and part are determined by dividing by MSTechnician * Part, as shown in the table above. The F-value for the interaction term is determined by dividing by MSE, and Minitab follows the same approach.

If the interaction term is not significant and is removed from the model, the F-values for the technician and parts are determined by dividing by MSE. This is also how Minitab handles it. You can observe both scenarios in the Minitab table above.

Thanks

Reply

Hi,
Thanks for your reply.

My comments are referring to the Calculations for 2 factor ANOVA with replication i.e. interaction included.
As I understand it we first have to do ANOVA with replication as we do not know the p value of the Tech*Part Interaction i.e. is it is to be ignored or not.
The excel table using the 2 factor with replication is shown below.

ANOVA
Source of Variation SS df MS F P-value F crit
Parts 116.529 9 12.948 215.45 0 2.040
Tech 0.1 2 0.05 0.831 0.440 3.150
Parts*Tech 0.447 18 0.0248 0.4130 0.980 1.778
Error 3.606 60 0.0601

Total 120.68196 89

In this calculation the F values for parts and Tech are obtained by dividing by MSError and MSParts*Tech,

As per my understanding the calculations in your table in the article showing manual calculations uses 2 factor ANOVA with replication and should correspond to the Excel Table. Herein this therefore MSError should be used in the denominator.

The conclusion that p>.05 for Tech* part interaction and therefore it should be ignored is given below this table. If this is OK then we can go on to calculate in the next step the table without interaction.

Sorry to bug you. But it is in the interest of a clear understanding.

Rgds,
Niraj

Reply

Hi,
Refer my earlier message. Unfortunately the Excel table was typed as a table but in acceptance the format was changed by your software into non tabular type.
Hope you are able to align the data into a table or else give me an email where I can drop my comments with the table reading as a table.
Rgds,
Niraj

Reply

Mr. Hessing,

Thank you very much for such clear and extensive article.

It was a great guide to me. I was working on a new Python package called pypetb for RnR análisis and this article was a big help checking its behaviour.

Reply

Ted, it was great.
Question, what part tolerance has to do in GRR? adding tolerance is optional in GRR and it shows in the column next to %study Var. i don’t know how to interpret it. what is the benefit of % Tolerance (SV/Toler).

An auditor was asking for it and says why you didn’t add it in GRR!!
I said have it or not doesn’t make changes in study but he was pushing us to add it

Reply

Hello Ali,

The %Tolerance (SV/Toler) column in the Gauge R&R (GRR) study indicates the percentage of total variation attributable to the tolerance of parts being measured. A high %Tolerance value suggests that much of the measurement variability is due to the allowed tolerance range for the parts themselves, while a low value indicates that the measurement system contributes less to overall variability.

This metric helps in understanding the measurement system’s performance relative to part tolerances and guides decisions for improving accuracy and precision.

It provides insights into sources of variation, aiding in optimizing the measurement process and ensuring compliance with quality standards.

Thanks

Reply

I have question about entering the correct Upper and Lower Spec Limit for a Minitab calcuation for a variable Anova Crossed Gauge R&R. This is an automated system we are evaluating where it is designed to reject parts with a gap greater than 0.8mm. So it accepts 0.0mm to 0.8mm. But it can get parts with a 1.3mm gap, and of course it should reject them. I initially preparred samples from 0.2(smallest that can be reasonable made) to 1.3mm, and ran the Gage R&R entering LSL = 0 & USL = 0.8. The system capability “Total Gage R&R” was much higher than we typically allow. I realized that it is elevated because some of my parts are above USL. If I enter LSL = 0 & USL = 1.3 with the same data, then it reduces Total Gage R&R by 30%. Which is the correct LSL and USL to get an accurate result? I’m asking because we had SOP’s that require a maximum Total Gage R&R, but it doesn’t explicetely state if LSL & USL are for the limits on the part being measured or limits of the system that is measuring the part. Thank you for your advice and input.

Reply

Hello Brad,

If the goal is to assess the system’s capability to measure parts within specified tolerances, the Upper Specification Limit (USL) and Lower Specification Limit (LSL) should align with the part specifications, which, in this case, range from 0.0mm to 0.8mm for accepted parts. However, if the aim is to evaluate the system’s ability to handle all possible scenarios, including measurements beyond the specified limits, then the actual measurement range of the system should be considered, extending up to 1.3mm in this instance.

Therefore, please consult with relevant stakeholders to determine the most appropriate approach to ensure an accurate interpretation of results.

Thanks

Reply

What distinguishes the %Tolerance analysis from the %Total Variation analysis? Additionally, how can we determine which approach (TV or tolerance) to employ in our process?
Thanks in advance.

Reply

%Tolerance analysis and %Total Variation (TV) analysis are both used to assess process variations, but they focus on different aspects.

%Tolerance Analysis

  • Purpose: %Tolerance analysis focuses on the allowable variation in a process relative to the total specification limits. It assesses whether the variations fit within the defined tolerances.
  • Application: Typically used in quality control and assurance to ensure product dimensions or characteristics meet specified limits.
  • Calculation: It is calculated as the ratio of the process variation (usually standard deviation) to the tolerance range, expressed as a percentage.

%Total Variation Analysis

  • Purpose: %Total Variation analysis examines the overall process variation, including common cause and special cause variations. It looks at the total variability present in the data.
  • Application: Useful in process improvement efforts, such as Six Sigma, to understand where variations come from and how to reduce them.
  • Calculation: This analysis often involves statistical techniques to decompose the total variation into components (like variance) and express how much of the total variation is attributed to different sources.

Choosing Between %Tolerance and %Total Variation Analysis

  1. Objective:
    • If your goal is to ensure product specifications are met, use %Tolerance analysis.
    • To improve the process and reduce variability, go for %Total Variation analysis.
  2. Stage of Process:
    • Early in product development, %Tolerance analysis may be more relevant to ensure designs are manufacturable within specs.
    • In later stages, particularly during optimization, %Total Variation can provide insights into process stability and improvement opportunities.
  3. Nature of Data:
    • If the data is strictly related to meeting specifications, %Tolerance is appropriate.
    • If the focus is on understanding overall process performance and variations, then %Total Variation is better suited.
  4. Regulatory Requirements: Sometimes, industry standards or regulations may dictate the type of analysis that must be performed.

Ultimately, the choice depends on the specific goals of your analysis and the characteristics of the process in question.

Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.