Other designed experiment types cover the one-factor designs (randomized block plans, Latin square designs, Graeco-Latin designs, and Hyper-Graeco-Latin designs) and also various mixture designs, orthogonal and balanced designs.

Randomized block plans
Randomized block designs are experimental block design that helps determine any variables that may or may not affect the data. When the objective is to compare more than two populations, the experimental design that decreases the variability within the samples is called a randomized block design. It is an extension of the completely randomized design (CRD).
A completely randomized design is useful when the experimental units are homogeneous. However, if the experimental units are heterogeneous, blocking is an option to form homogenous groups.
Many randomized block plans and screening experiments cannot analyze interactions.
Block
When groups of experimental units are similar, grouping the similar units is a block. By blocking, one can decrease the variability within each group, which allows for detecting the differences caused by the treatments more clearly.
Blocks in the experiment are to control the effects of some nuisance variables (like cholesterol level, weight, age, etc.) by bringing that variable into the experiment so that some of the variability in the experiment can be reduced.
Blocking in experimental design is similar to stratification in sampling.
Example:
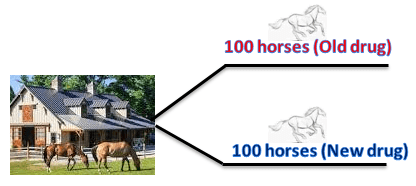
200 horses are living in a horse barn. The doctor wants to compare the impact of a new drug vs. the old drug.
Case 1 – Completely randomized design: The doctor randomly grouped 100 horses and treated them with a new drug, and similarly, the rest of the 100 horses with an old medication.
Case 2 – Randomized block plan: A doctor segregated horses breed-wise and then treated them with old and new drugs to test the effectiveness and compare the results among the breeds.
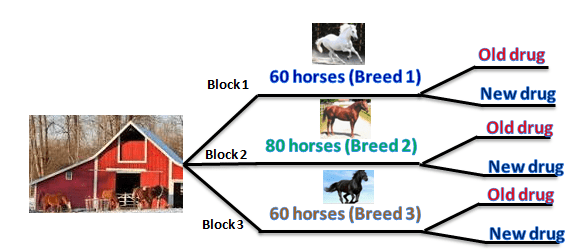
In a completely randomized design, the doctor treated the horses with an old and new drug; different breeds may react differently to the drug. In a randomized block design, same-breed horses are randomly treated with an old and a new drug. Compare the results among the breeds.
Hence Randomized block design tends to provide a better estimate of the true error variance and leads to a more powerful hypothesis test in terms of the ability to detect the difference among breed means.
Simplex-lattice designs
When a product is formed by mixing various ingredients, then the product is called a mixture, and the ingredients are called mixture components. The four common design types in the mixture design are simplex lattice, simplex centroid, simplex axial, and extreme vertex.
The simplex lattice design is a common design method for a small number of components with response surfaces that need a polynomial function. Furthermore, this function represents how the components affect the response. To study the shape of the response surface, the usual design choice would be points spread evenly over the whole simplex. The uniformly spaced point distribution on a simplex is known as a lattice.
Example: 3 components mixture simplex-lattice design
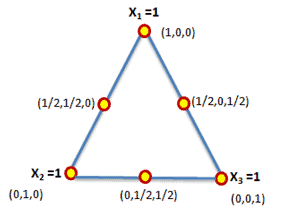
Define evolutionary operations
Evolutionary operations methodology are also referred to as EVOP is a design of experiment (DOE) statistical method to improve the process or product quality. This process was first developed by Geroge Box in 1957.
The basic purpose of the evolutionary operations methodology (EVOP) is to improve a process through systematic changes in the operating conditions of a given set of factors. See evolutionary operations here.
Latin Squares
A Latin square is an nxn array of n different symbols (like A, B, C,…) such that each object occurs only once in each row and only once in each column. Furthermore, the Latin square design is a fractional factorial experiment that requires less experimentation to determine the main treatment results.
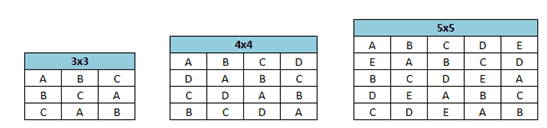
The factors in Latin square design are row, column, and treatments
The number of treatments = No.of rows= No.of columns =n
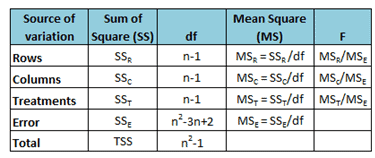
Total sum of squares (TSS) = SSR+SSC+SST+SSError
Two major conditions of Latin square design:
- The number of rows, columns, and treatments must be the same.
- No expected interactions between row and column factors.
We also call a Latin square design a one-factor design because it attempts to measure the effects of a single key input factor of an output factor. The experiment further attempts to block the effects of two or more nuisance factors.
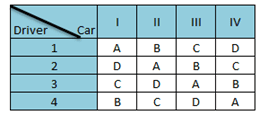
Example: Four drivers (1,2,3, and 4) and four cars (I, II, III, and IV) were used to evaluate the mileage from four oils (A, B, C, and D). For example, the first cell indicates driver 1 will use oil A for Car I.
The Anova Table of Latin Square design
Graeco-Latin Square Design
Graeco-Latin square design is similar to Latin square design, but in some designs where the experimenter needs to block in three directions, it is also useful to eliminate more than two sources of variability in an experiment.
Example: A pharmaceutical laboratory is measuring the effectiveness of five various procedures when determining the mean amount of calcium in medicine. Five chemists test five batches of medicine with five different apparatuses to determine the mean amount of calcium.
5X5 Graceo-Latin Square design
- Procedures – A, B, C, D, E
- Chemists – α, δ, β, γ, λ
- Apparatus – 1,2,3,4,5
- Medicines – Φ, Ω, Χ, Ψ, σ
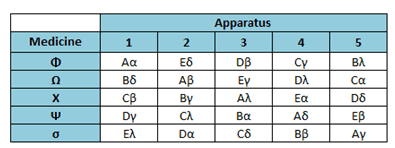
- Each upper case letter (method) appears only once in each row and column
- Greek letter (chemist) appears only once in each row and column
- Each pair of upper case and the greek letter appears only once in the entire square
- Final result – Each chemist uses each procedure only once, analyzes each medicine only once, and uses each apparatus only once.
Hyper-Graeco-Latin Square
A Hyper-Graeco-Latin Square design is to study treatments with more than three blocking factors. One of the efficient designs to study the effect of one primary factor in the presence of more than three blocking factors. However, they are restricted to the point in which all factors have the same levels.
Example: 4X4 Hyper-Graeco-Latin Square design
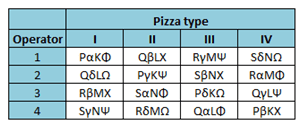
- Dough: P, Q, R, S
- Oven: K, L, M, N
- Time: α, δ, β, γ
- Flour: Φ, Ω, Χ, Ψ
Latin Square: is a type of fractional factorial design. Fractional factorials (like Latin and also Graeco-Latin Squares) will not allow the analysis of interactions. Furthermore, the interactions are confounded with other effects.
Linear & Quadratic Mathematical Models
The main effect measures the average change in the response when the control factor varies from the minimum to the maximum settings. At the same time, interactions occur when the impact of a one-parameter depends on the setting of another parameter.
A mathematical model of the process can generate by using the experimental design. Furthermore, the analysis of experimental design studies uses multiple linear regression to fit a polynomial model to the experimental data.
For a response y, the mathematical equation is as follows:
Y =b0 +b1A+ b2B+b3C+b12AB+b13AC+b23BC+b11A2+b22B2+b33C2+ᵋ
Y is the predicted response, b0 is the model constant; b1, b2, and b3 are linear coefficients; b12, b13, and b23 are cross product coefficients, and b11, b22, and b33 are the quadratic coefficients.ᵋ error term.
Balanced & Orthogonal Designs
Orthogonal Design: An experimental design is orthogonal if each factor can evaluate independently of all the other factors. In other words, a given design’s main and interaction effects can be estimated without confounding the other main effects or interactions.
For example, two vectors can be treated as orthogonal if the sum of the products of their corresponding elements is 0.
Example: Check whether vectors a and b are orthogonal.
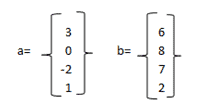
The product of a*b = 3*6+0*8+-2*7+1*2=0
Hence the vectors a and b are orthogonal.
Balanced Design: Balanced design implies that the data distribute properly over the design space. In other words, a balanced design has an equal number of observations for all possible level combinations. It implies a uniform physical distribution of the data and an equal number of levels of each factor.
Example: A two-level full factorial balanced design with two factors (Pressure & Temperature) and also with two replicates.
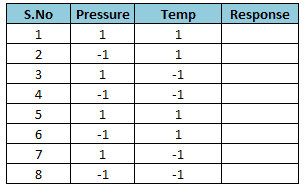
Particularly balanced design will have the same number of observations for all possible combinations of factor levels for pressure and temperature.
Fit, Diagnose Model, and Center Points
Center points are the experimental runs where the inputs are set in the center (halfway) between the minimum and maximum settings.
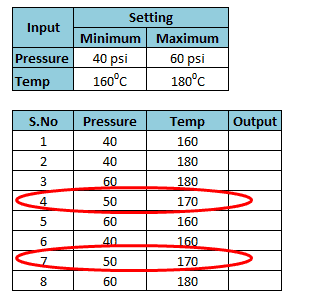
Example: Center point would be midway of pressure 50 psi and temperature 170 degrees centigrade.
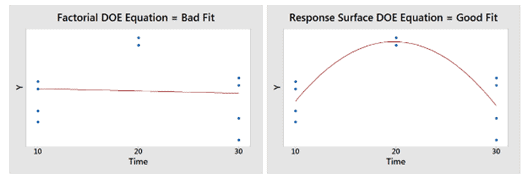
Center points also use to detect the curvature. If in case a center point is significant, then the experimenter needs to use the Response Surface method to analyze data.
Additional Resources
- http://www.itl.nist.gov/div898/handbook/pri/section1/pri11.htm (Linear & Quadratic Mathematical Models)
- http://www.itl.nist.gov/div898/handbook/pri/section3/pri336.htm (Linear & Quadratic Mathematical Models)
- http://www.micquality.com/six_sigma_glossary/balanced_design.htm (Balanced design)
- http://www.itl.nist.gov/div898/handbook/pri/section3/pri337.htm (Center point)

