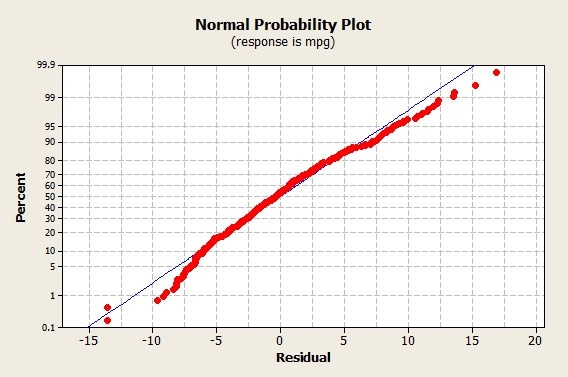
The normal probability plot is a graphical technique for normality testing: assessing whether or not a data set is approximately normally distributed. In other words, a normal probability plot is a graphical technique to identify substantive departures from normality.  The normal probability plot is one type of quantile-quantile (Q-Q) plot.

A Normal Probability Plot compares the values in a data set (on the vertical axis) with their associated quantile values derived from a standardized normal distribution (on the horizontal axis). In other words, it plot graph Z-scores against the data.

Why Do You Use a Normal Probability Plot?

The normal probability plot is formed by plotting the sorted data with an approximation to the means or medians of the corresponding order statistics, and we do this because it helps us visualize the data. We use a normal probability plot in order to determine if a small set of data comes from a normal distribution. In other words, if we get a straight line from the plot, we can say the process is normally distributed. Thus, it is an excellent option to determine the Process capability.

When Do You Use a Normal Probability Plot

The data are drawn against a theoretical normal distribution in a manner that the points should form almost a straight line. Departures from this straight line indicate departures from normality. This includes identifying outliers, skewness, kurtosis, a need for transformations, and mixtures.

How to Construct a Normal Probability Plot

1. Firstly, arrange the values in ascending order. In other words, arrange the n number of values from minimum to maximum.

2. Secondly, arrange a rank order number(i) from 1 to n. Here n is the total number of samples

3. Thirdly, calculate the cumulative probability for each rank order from1 to n values

For example: f(i) = (i-0.375)/(n+0.25)

4. Then, for each cumulative probability value, determine the z-value from the standard normal distribution.

5. Next, create a scatter plot with the sorted data versus corresponding z-values

6. Finally, analyze the graph. If all the points are roughly on a straight line, then determine if it follows the normal distribution.

Example of Using the Normal Probability Plot in a Six Sigma Project

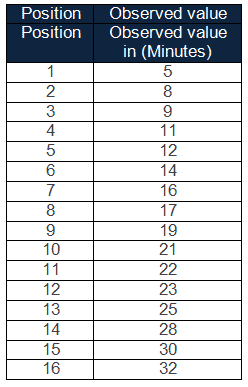
Example: The data in the table below is a random sample of 16 individuals’ wait times in the coffee shop. Is there evidence to support the belief that the variable of waiting time follows a normal distribution?

Step 1: Arrange data in ascending order

Step 2: Then, assign a rank order number(i) from 1 to n. For instance, the total number of samples n equals 16.

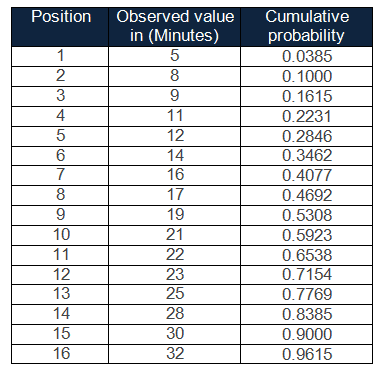
Step 3: Calculate the cumulative probability

f(i) = (i-0.375)/(n+0.25)

for i=1, f(1) =(1-0.375)/(16+0.25) = 0.0385

for i=2, f(2) = (2-0.375)/(16+0.25) = 0.1000, similarly calculate for other values.

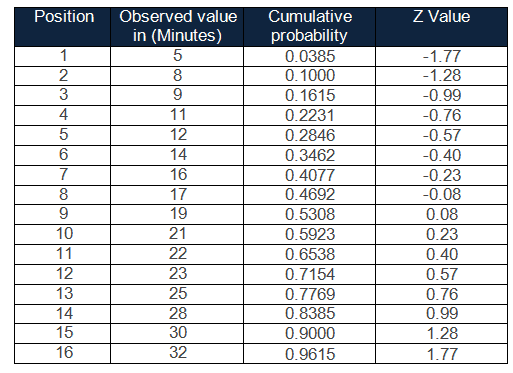
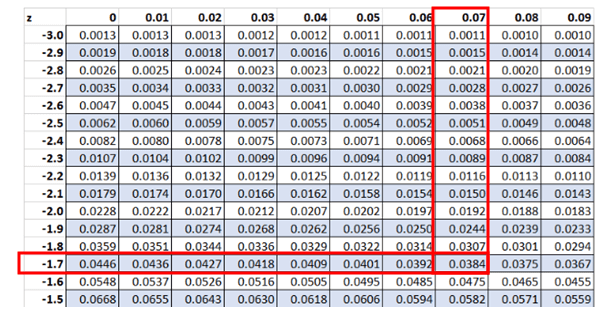
Step 4: Further, determine the z value for each cumulative probability

Step5: Then, create a scatter plot with the sorted data versus corresponding z-values

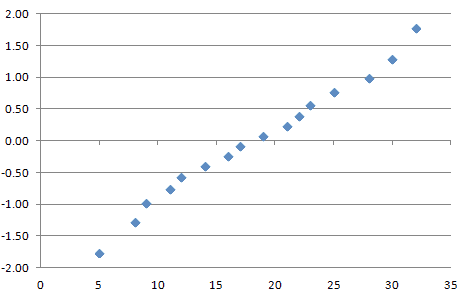
Step 6: Analyze the graph: To explain, from the above graph, it is almost clear that the Normal probability plot is close enough to linear. Hence we conclude that wait time follows a normal distribution.

Important Videos