Hypergeometric Distribution

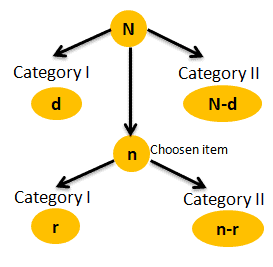
The Hypergeometric distribution is a discrete distribution that specifically measures the probability of a specified number of successes in (n) trials, without replacement, from a relatively large population (N). In other words, a sample size of n is randomly selected without replacement from a population of N items.

The hypergeometric distribution is an example of a discrete probability distribution because there is no possibility of partial success; that is, there can be no poker hands with 2 1/2 aces. 

Difference between Binomial and Hypergeometric distribution

The hypergeometric distribution similarly resembles the binomial distribution. Likewise, the probability is the same for all the trials. Furthermore, we assume the probabilities (p and 1-p) that represent the average probabilities from a large number of independent observations. In binomial distribution, the probability of success is the same for all trials, while it is not the case for hypergeometric distribution. 

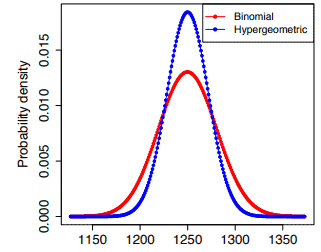
The hypergeometric distribution is suitable for describing a finite and probably small population, and also, the population is divided into separate categories. In other words, the sample size is relatively large when compared to the population count. Furthermore, hypergeometric distribution is used to test the probabilities for dependent trials.

Hypergeometric distribution formula

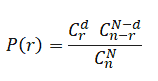
• Firstly, d= possible number of successes
• Secondly, N= Population size
• Thirdly, n= number of trials
• Fourthly, r= number of successes in n trials
• Finally, P(r) = probability of observing r success in n trials

Mean µ = d*n/N

Standard deviation = √((d(N-d)*n(N-n)/((N²(N-1))))

Assumptions

• The number of objects in the population N  to be much larger than the number of objects in the sample n.
• The number of two types of objects in the population d and N-d are much larger than the sample n.
• However, we are not assuming that n or r large.

Properties of Hypergeometric distribution

• Firstly, it is a discrete distribution.
• Secondly, the probability of success changes from trial to trial.
• Thirdly, the successive trials are dependent.
• Fourthly, it has three parameters N,n, and d.
• The mean of hypergeometric is always greater than the variance.

Hypergeometric Distribution Example

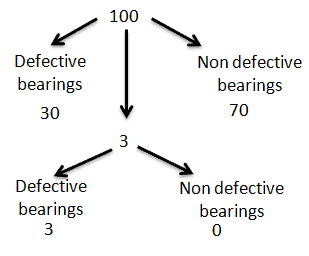
Example 1: A container contains 30 defective bearings and 70 non-defective bearings. A random sample of three bearings is drawn from the container, and afterward, it is replaced. So, what will the probability that the three bearings are defective? Also, calculate the mean and standard deviation.

• d= 30
• N= 100
• N-d =70
• n= 3
• r= 3

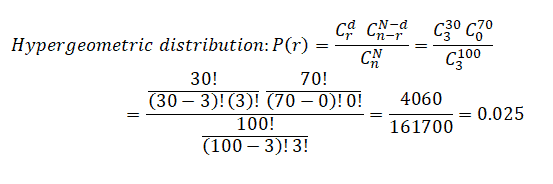
Mean µ = d*n/N = 30*3/100 =0.9

Standard deviation = √((d(N-d)*n(N-n)/((N²(N-1)))) =√(30(70)*3(97)/ 100²(99)) =0.78

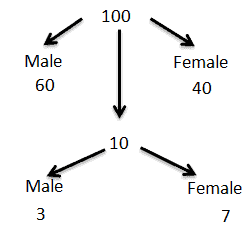
Example 2: XYZ Manufacturing unit is conducting union leader elections for each plant straightaway. For example, if plant one contains 60 male and 40 female workers or voters. Then, a random sample of 10 voters is drawn. Following this data, what is the probability exactly three will be male voters?

• d= 60
• N= 100
• N-d =40
• n= 10
• r= 3

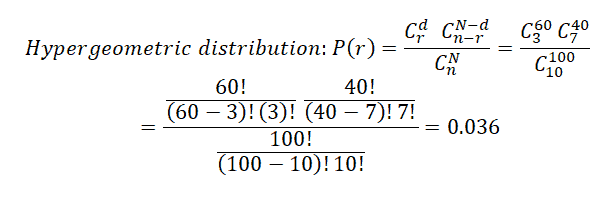
Hypergeometric Equation Excel Template

Important Videos