The Exponential Distribution is one of the widely used continuous distributions. It estimates the lapse of time between independent events. In other words, it describes the times in between events, a process in which events occur continuously and independently at a constant average rate.

The Exponential Distribution is the time between events in a Poisson process. Simply, it is an inverse of Poisson. If the number of occurrences follows a Poisson distribution, the lapse of time between these events is distributed exponentially. It is used to model items with a constant failure rate.

The exponential and gamma distributions are related. Gamma distribution estimates the waiting time for more than one event, whereas the exponential distribution estimates the time between independent events.

Key differences between Poisson and Exponential.

The formula of Exponential Distribution

The Probability density function (pdf) is

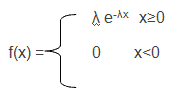
• Where e is base natural logarithm = 2.71828
• λ is the mean rate of occurrence
• x is a random variable

The Cumulative distribution function (cdf) is

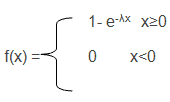
The mean and Variances are

Mean = 1/λ

Variance = 1/λ²

The exponential distribution is unilateral. In other words, it is one dimension or only positive side values. If it is a negative value, the function is zero only.

Shape of the Exponential distribution

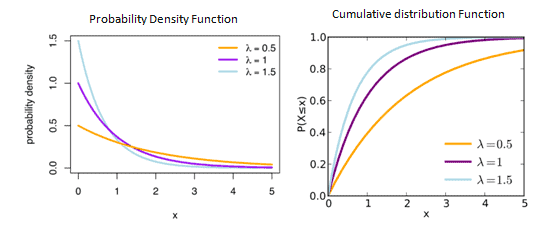
The distributions of a random variable following exponential distribution is shown above. The curve declines continuously, implying that as x rises, the probability attached to it decreases.

When is the Exponential Distribution used?

• Describes the times in between events, a process in which events occur continuously and independently at a constant average rate.
• To describe the time between successive occurrences when all occurrences follow an exponential.
• To predict the length of time that properly maintained equipment will operate.
• Also, approximate the time between outcomes. (See Poisson)
• When a probability of an outcome is consistent throughout the time period.

Applications

The exponential distribution estimates the time lapse between two independent events in a Poisson process. It can model a variety of events  and can provide solutions for daily life problems:

• The number of hours a mobile phone runs before its battery dies out.
• The time it takes for a call center executive to respond to a caller
• The probability of receiving a phone call in the next thirty minutes
• The amount of time (maybe in months) a car battery lasts.

Exponential distribution Example

Example: The length of service in the drive-thru has been exponential distribution and found an average to be 10 minutes. If a car arrives at the drive-thru just before you, find the probability that you will wait for:

• Less than 5 minutes
• Between 5 and 10 minutes
• Greater than 10 minutes
• Variance

The average is 10 minutes; hence λ=1/10

Case 1: Less than 5 minutes

P(X<x) = 1- e^-λx   

So, P(x<5)  = 1- e^(-1/10)*5    = 1- e^-0.5 =   1-2.71828^(-0.5) =0.3934

Case 2: Between 5 and 10 minutes

P(x<5)  =0.3934

P(x<10)  = 1- e^(-1/10)*10    = 1- e^-1 =   1-2.71828^(-1) =0.6321

So, P(5<x<10) = P(x<10) – P(x<5)  =0.6321-0.3934 = 0.2386

Case 3: Greater than 10 minutes

P(X>x) = 1-P(X<x)=1-(1- e^-λx  ) = e^-λx

So, P(x>10)  = e^{(-1 / 10) * 10}    = e^-1=  2.71828^(-1) =0.3678

Variance = 1/λ² = 1 / ( 1 / 10)² =100

Important Videos

Six Sigma Black Belt Certification Questions:

Question: If a process follows an Exponential Distribution with a mean of 25, what is the Standard Deviation for the process? (Taken from ASQ sample Black Belt exam.)

(A) 0.4
(B) 5.0
(C) 12.5
(D) 25.0

Answer:

D: 25.0. In an exponential, the mean and Standard Deviations are equal.