In Design of Experiments, blocking involves recognizing uncontrolled factors in an experiment–for example, gender and age in a medical study–and ensuring as wide a spread as possible across these nuisance factors. Let’s take participant gender in a simple 3-factor experiment as an example.
| Trial | Factor A | Factor B | Factor C |
|---|---|---|---|
| 1 | – | – | – |
| 2 | + | – | – |
| 3 | – | + | – |
| 4 | + | + | – |
| 5 | – | – | + |
| 6 | + | – | + |
| 7 | – | + | + |
| 8 | + | + | + |
The basic steps we need to follow in order to successfully block this factor in an experiment are:
- Determine how many trial blocks we need. The existing trials need to be divided by the number of levels in the uncontrolled factor. In the case of gender, this would generally be two ‘blocks’ of trials.
- Ensure proper distribution. It’s not enough to just distribute trials into blocks at random, or en masse – this can mess up our results. We can use a blocking scheme to figure out a good distribution pattern.
The standard blocking scheme for a 3-factor 2-level experiment looks like this: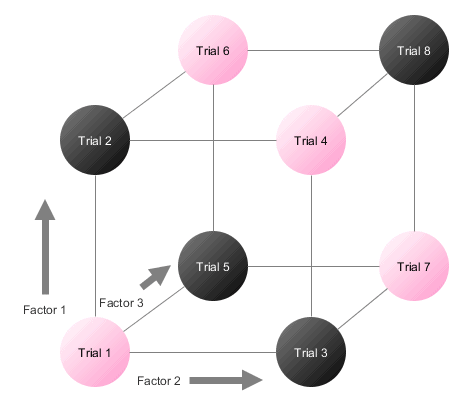
Design of Experiments: Blocking Dividing the trials this way–with each block assigned a different color–ensures that you get an even distribution across all factors, not just one or two.
- Design the experiment. Once you’ve assigned a color to a block, you can add blocking into your experiment design:
Trial Factor A Factor B Factor C Gender 1 – – – Male 2 + – – Female 3 – + – Female 4 + + – Male 5 – – + Female 6 + – + Male 7 – + + Male 8 + + + Female

