Let’s say you work in a TV manufacturing plant as a QA inspector in the final inspection. As flat-screen TVs come off the production line, you check for defects or defective products. Firstly, how would you measure defects? Secondly, would you count the number of scratches or the number of broken pixels on the screen? Also, does the size of the scratches matter? What if one of the TV screens is smaller than the other or the display colors are off? All of these questions relate to Scales of Measurement.

What is It?

Simply put, Scales of Measurement classify your data into four categories. Those four categories are Nominal, Ordinal, Interval, and Ratio. This article will dive into more details on each scale. The most important thing to know about Scales of Measurement is that the Nominal Scale is the easiest to gather data but provides minimal insight into the data. In contrast, the Ratio Scale is more complex but leads to better data analysis.

Nominal Scale of Measurement

Think of categories when you see the Nominal Scale. For example, you may categorize the color of an object, whether small or big, where someone traveled for vacation. Nominal Scales never include a number. Nominal Scales can also separate data into YES/NO, GO/NO GO categories.

Therefore, Nominal Scales of Measurement are very simple. These data types cannot be divided or multiplied as you would in Ratio or Interval scales. There is also no order to the data.

According to our TV example, Nominal Data for quality acceptance could be:

• PASS/FAIL (If the TV is defective or not)
• Tall, short, or wide
• Heavy or light

Ordinal Scale of Measurement

Just as the name implies, ORDER is important in ORDinal scales. This also includes a ranking of something such as:

• First place, second place, and third place in a race
• Cold, Warm, Hot, Hottest

Ordinal Scales are similar to Nominal Scales, but the biggest difference is that order matters in Ordinal Scales.

Consider, for instance, our TV example; the Ordinal Scale could be used to organize the TVs inspected from most defects to least defects. However, gathering defect data using Interval or Ratio Scales would be more beneficial, as you’ll see further on.

Helpful links for Ordinal Scale of Measurement:

• https://corporatefinanceinstitute.com/resources/knowledge/other/ordinal-data/
• https://www.formpl.us/blog/ordinal-data

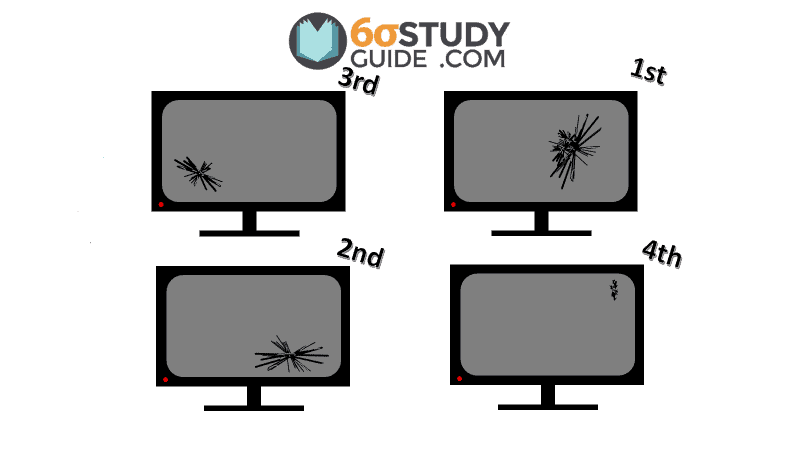
Interval Scale of Measurement

An interval involves numbers with a meaningful difference between each value. There is order, and the difference between the two values is meaningful. However, you cannot always double the value of something in an interval scale and claim it is twice the size of its original value. A good example of this is Credit Scores. Credit Scores range between 300 to 850. You cannot double your credit score of 300 to 600 and claim to a bank teller that a score of 600 is twice as good as a score of 300. In addition, you cannot double your score from 600 to 1,200 because a score of 850 is as high as you can go.

For instance, other existing Interval Scales include:

• Temperature (Fahrenheit or Celsius)
• Time
• Credit Score
• Test Scores
• pH levels

In Interval Scales, there is a starting point. Consider cumulative GPAs in the US education system. Each student starts with a 4.0 GPA. By earning A’s in classes, you maintain a 4.0 GPA. Class grades less than an A cause your cumulative GPA to drop below 4.0. This differs from Ratio Scales because Ratio Scales do not have an inherent starting point. In other words, Ratio Scales have an absolute zero.

I mentioned earlier how ranking defects in TVs using an Ordinal Scale doesn’t make much sense. It would be better to use the Interval Scale so that we can quantify the number of defects in TVs rather than apply an obituary rank of “most/least defects” on a TV.

Helpful links for Interval Scale of Measurement:

• https://www.questionpro.com/blog/interval-data/
• https://www.formpl.us/blog/interval-data
• http://www.intellspot.com/interval-data-examples/

Ratio Scales of Measurement

Ratio Scales are very similar to Interval Scales. The key difference, though, is Ratios have a clear definition of what 0 represents. When something is 0 on the Ratio Scale, that means it doesn’t exist. In comparison, Interval scales such as temperature, something that is 0* Celsius, means the water is at a point of freezing.

Multiplying and dividing a figure creates a meaningful difference in Ratio Scales. Let’s take the weight as an example. You can quantify the difference between an item that is 2 kilograms versus an item that is 10 kilograms. The item that is 10 kilograms is 5x heavier than the 2-kilogram object.

Other examples of Ratio Scales include:

• The Metric System (meters, centimeters, etc.)
• Imperial System (inches, foot, mile)
• Volume (gallons or quarts)
• Speed (Miles/hour or Kilometers/hour)

We can better define defects found on our TVs with Ratio Scales. We are no longer counting defects, but we can measure them to understand the defect’s impact.

For example, applying the ratio scale to our TV concept means we are sizing each defect. We measure the size of a scratch on the screen or the size of missing pixels on the monitor. We measure the exact dimensions of the monitor to confirm it meets customer specifications. All in all, the use of ratio scales allows us to dig into the nitty and gritty details of the defects.

Why Ratio is Best for Six Sigma:

Ratio Scales are ideal for Six Sigma because they provide descriptive statistics, enabling us to analyze the data more completely. As Six Sigma professionals, it is impossible to reach a Six Sigma performance level in a process unless we can fully map out the collected data.

That’s not to say the other scales don’t have a place in data collection. In fact, all four scales are usually gathered at the same time, depending on the project’s scope. Consider, for instance, a car that is built for a customer. That car can meet all customer specs of size and weight, but if it isn’t the correct color, it is looked at as a failure in the eyes of our customers. And guess what? Color comes from the Nominal Scale!

Scales of Measurement Videos