Poisson distribution is a Discrete Probability distribution; it describes the mean number of events happening in a fixed time interval.  The Poisson Distribution is a discrete distribution that is often grouped with the Binomial Distribution. Simeon Poisson, a French mathematician, first created the Poisson distribution in 1781.

The mean number of occurrences in the Poisson distribution is denoted by λ. Unlike Binomial Distribution, Poisson distribution continues forever and is bounded by 0 and ∞.

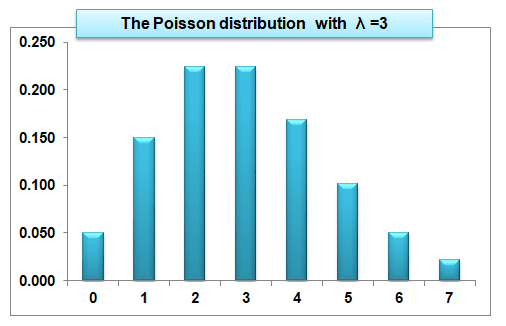
The Poisson Distribution is quite useful when you need to know the probability of an event that occurs randomly in some unit of measure (e.g., the number of traffic accidents at a particular intersection per month).

When to use the Poisson Distribution:

Poisson distribution is a discrete function. It measures only occurring or not occurring. In other words, it measures only whole numbers, not fractions. Example: number of telephone calls in a month. Poisson distribution is also a very handy distribution as it takes only one parameter.

Assumptions of Poisson Distribution

• The probability of an occurrence is constant over time. In other words, the rate does not change based on time.
• Occurrences are independent. In other words, the occurrence of one event does not affect the occurrence of a subsequent event.
• It is also a discrete probability distribution.
• No upper limit to the number of occurrences of an event during the specified time interval.
• The probability of a single occurrence of an event within a certain time period is proportional to the length of the time period.
• The probability of each occurrence is less than 0.1.
• It is a positively skewed distribution.

The Poisson Equation

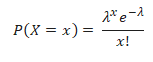
Where

• e is the base neutral logarithm (2.71828)
• λ is the mean number of occurrences
• x is the number of occurrences in question

Example of Poisson Distribution

XYZ is a call center with an operational process with a 3.5% error rate. So, what is the probability of k (0, 1, 2, 3, 4, 5) errors?

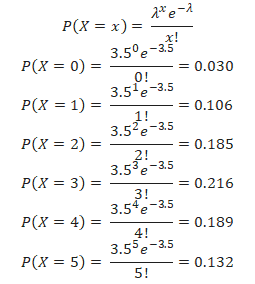
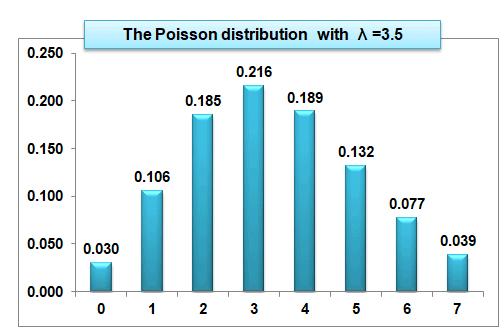
Poisson and Time Intervals

For instance, if the number of occurrences of some event follows a Poisson distribution, the time between successive occurrences will follow an Exponential Distribution.

In probability theory and statistics, the exponential distribution (a.k.a. radical exponential distribution) is the probability distribution that describes the time between events in a Poisson process, i.e. a process in which events occur continuously and independently at a constant average rate.

http://en.wikipedia.org/wiki/Exponential_distribution

Poisson Distributions Example Questions

When we hear “What is the probability of occurrences?” in a question, we know it’s time to use Poisson. Also, there are examples of seeing or hearing the word ‘PER.’

• What is the probability of zero occurrences?
• Bugs PER megabyte of code
• Number of ‘sick days’ PER school year

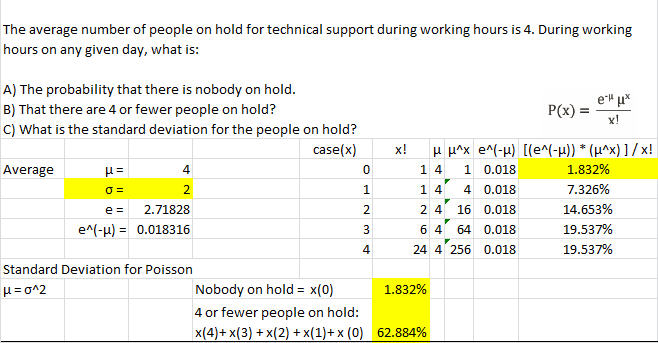
Example 1 (Nobody, Or fewer, Standard Deviation)

The average number of people on hold for technical support during working hours is 4. During working hours on any given day, what is:

A) The probability that there is nobody on hold?
B) That there are 4 or fewer people on hold?
C) What is the Standard Deviation for the people on hold?

Example 2 (or more)

A large city has an average of 2.4 fatal car wrecks per week. So, what is the probability that there are 3 or more fatal car accidents?

Example 3 (Less than)

A farmer has an average of 7 weeds per acre on his farm during the summer months. On any acre in the summer, what is the probability that the farmer has less than 3 weeds?

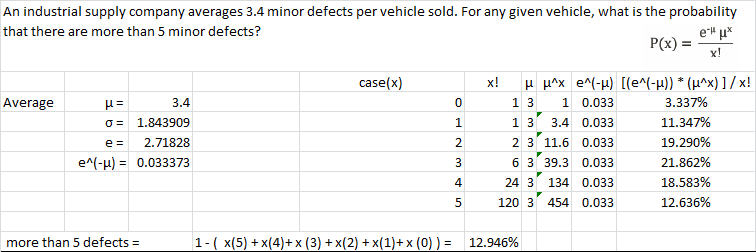
Example 4 (More than)

An industrial supply company averages 3.4 minor defects per vehicle sold. For any given vehicle, what is the probability of more than 5 minor defects?

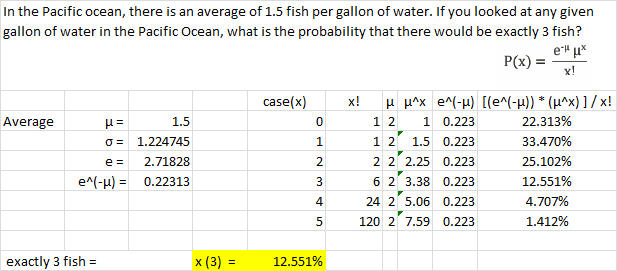
Example 5 (Exactly)

The Pacific Ocean has an average of 1.5 fish per gallon of water. If you looked at any given gallon of water in the Pacific Ocean, what is the probability that there would be exactly 3 fish?

Poisson Videos

Other Good Poisson Distribution References here:

http://www.six-sigma-material.com/.html

http://ncalculators.com/math-worksheets/.htm

Six Sigma Black Belt Certification Poisson Distribution Questions:

Question: A process produces Nonconformities according to a Poisson distribution. If the mean of the Nonconformities is 25, what is the Standard Deviation?

(A) 2.5
(B) 5.0
(C) 12.5
(D) 25.0

Answer:

5.0  For Poisson distributions, the Standard Deviation is approximated by the square root of the mean. The square root of 25 is 5.